33First develop uniformity....
that is remove [] as it is horrible and convert the eqn in x and {}, {} is periodic and so much better..
Now eqn becomes 5{x}=2x
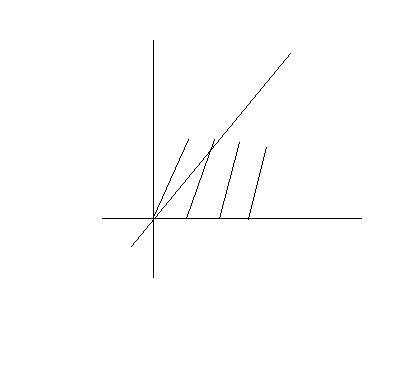
Now draw both graphs and intersections will come easily
5 Answers
3333
clearly two solns x=0 and something b/w 1 and 2...
Now some written work...
33for 1<x<2 {x}=5x-5
now 5x-5=2x
x=5/3
now 1<5/3<2 so correct
try some intervals also like 2<x<3 {x}=5x-10
5x-10=2x, x=10/3 but 10/3 >3 so no soln...
similalry for other intervals but you have to keep graph in back of ur mind if u not want to check many intervals
1whats wrong in my method
4x - 4[x] = x + [x]
3x = 5[x]
[x] = 3x/5
3x/5 ≤ x < 3x/5 + 1
0 ≤ x < 5/2
plzzz. correct me
@ Aman. You final inequality is correct.
0 ≤ x < 5/2
The solution of the given equation will lie in this interval [1]
But to find out the actual solution its better to change into 5{x}=2x ----- (1)
as Abhishek has written above.
Now 0 ≤ LHS < 5
And its clear from graph that in interval [0,1} it has only solution at x=0
There is another solution in [1,2} which can be calculated as intersection point of two lines
y=2x & y=5(x-1)
which gives x=5/3
beyond x≥3 , RHS is ≥ 6 but LHS ≤5 so no solution afterwards ...
Also you there is no solution in [2,3} as Abhishek has proved above.