2305Is it 3852?
Himanshu Giria I don't know but please show how....Upvote·0· Reply ·2014-04-06 04:32:01- Himanshu Giria Pls show how???
If f :N→N such that f(f(x))=3x;
Then find f(2013)
-
UP 0 DOWN 0 0 10
10 Answers
23052305Sorry I didn't post the full solution before.I had taken an assumption which I cannot prove.
The assumption was that f(x) is a strictly increasing function.
Anyways assuming that is true,here are some of the values of f(x).
f(n)≠n for all n.Because that would imply f(f(n))=n but we know that f(f(n))=3n.
Furthermore f(n)>n.
Because if f(n)<n then f2(n)<f(n) (since f(x) is increasing)
→3n<f(n).This leads to a contradiction.
From the above we can see that,
f(n)>n and f2(n)=3n>f(n)
→ 3n>f(n)>n
For n=1,
3>f(1)>1 →f(1)= 2
f(2) = f2(1) = 3
f(3) = f2(2) = 6
f(6) = f2(3) = 9
f(3)<f(4)<f(5)<f(6)
→6<f(4)<f(5)<9
Therefore,f(4) = 7 and f(5) = 8
After doing this for the first 20 numbers I found a pattern.
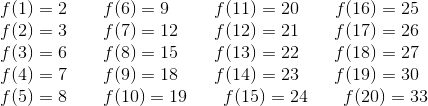
From here we can see that if
3k<n<2*3k then,
f(n) = n+3k
and if 2*3k<n<3k+1 then,
f(n) = 3n - 3k+1
You can prove this using induction.
Hence f(2013) = 3852
However the solution is not complete.Someone still needs to prove that f(n) is strictly increase(proving that it is strictly monotonic also can be helpful) because I'm pretty sure that the function is strictly increasing.
- Himanshu Giria thanks:)
466no one for this qn...??
- Himanshu Giria I don't know but please show how....
486f(x)=x√3 (Just observed it. I don't know the method)
f(2013)=2013√3
Akshay Ginodia actually f(x) can't be xroot3 as the function is defined from N to N