In the given fig. graph of y = p(x) = x4 + ax3 + b2 + cx + d is given.
If p(x) + c = 0 has 4 distinct real roots α , β , γ , δ then [α] + [β] + [γ] + [δ] is equal to
(A) -1
(B) -2
(C) 0
(D) 1
plzz give the full soln...
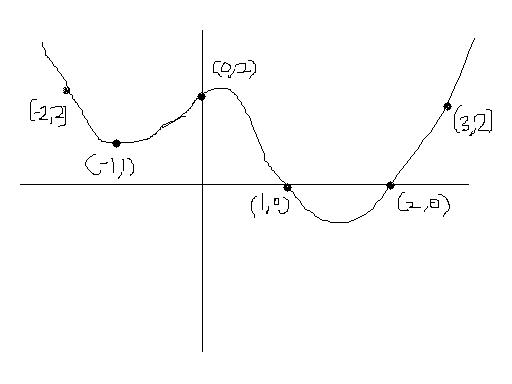
106the only way the graph of p(x) +c can have 4 distinct real solutions is when the graph is shifted downwards by an amount such that the left minima and the middle maxima are on opposite sides. i.e. value of function at left minima < 0 and value of function at middle maxima > 0.
try and figure it out urself
6nope jeetopper
it looks to be c but its not:P
the answer is a
thnx asish for the hint...