11) 2
1) Find the number of solutions of 2|x|=sinx2.
2) Find the area enclosed by: | x+y-1| + |2x+y+1|= 1
3) Find the number of solutions of tan4x=cosx when x lies between (0 to pie)..
PLEASE Provide the graph with the solution..
-
UP 0 DOWN 0 0 4
4 Answers
212.
Case 1:If both x+y-1 and 2x+y+1≥0
The eqn. becomes 3x+2y=1
So, X and Y Intercepts are 1/3 and 1/2 respectively.
Case 2:If x+y-1<0 but 2x+y+1≥0
The eqn. becomes x=-1
Case 3:If x+y-1≥0 but 2x+y+1<0
The eqn. becomes x=-3
Case 4:If both x+y-1 and 2x+y+1 are <0
The eqn. becomes 3x+2y=-1
Solving, we get four points (-1,2),(-3,5),(-1,1) and (-3,4).
Area=2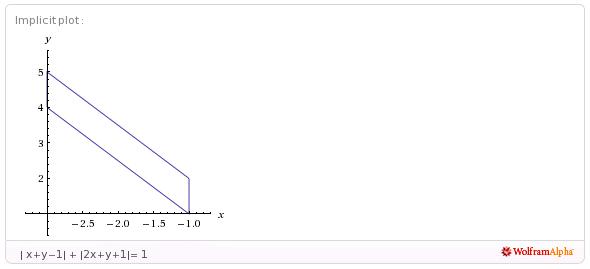
213.
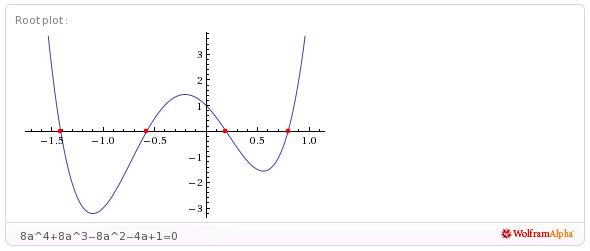
The eqn. is equivalent to
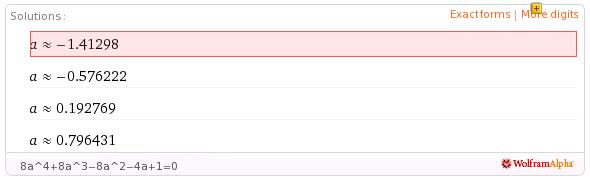
8a^4+8a^3-8a^2-4a+1=0
where a=sinx
Plot the graph and get the positive roots
sinx≈.2 and sinx≈.8
so, x≈arcsin(0.2) and x≈arcsin(0.8)
