INTEGERAL CALCULUS

well from my not-so-competent logic i can try to do this

i am first of all converting this to a definite integral for my convinience!

the integral is \int_{0}^{x}{\frac{x}{dx}}

considering the function y=x

so what we have to do is divide the graph into rectangles of breadth w and find the summation of l/b in the interval 0 to x

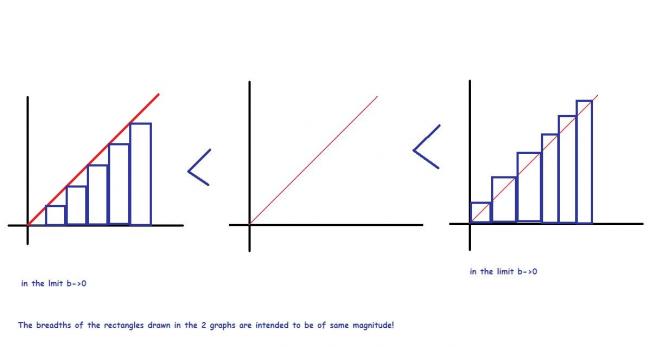
\lim_{b\rightarrow 0}\sum_{r=0}^{\frac{x}{b}}{\frac{r}{b}}\leq \int_{0}^{x}{\frac{x}{dx}}\leq \lim_{b\rightarrow 0}\sum_{r=0}^{\frac{x}{b}}{\frac{r+1}{b}}

i think using this concept we can solve this problem

completely unsure if this approach is even 0.01% correct! :P