1given is 2\int_{0}^{1}{(tan^{-1}x)^{2}}dx
\Rightarrow 2\int_{0}^{1}{(tan^{-1}x)(tan^{-1}x)}dx
taking first funtion any one and integrating byparts we get
\Rightarrow\left[ 2\left[tan^{-1}x\int{tan^{-1}x}dx \right]^{1}_{0}-2\int_{0}^{1}{\frac{\int tan^{-1}x}{1+x^{2}}}dx\right]
\Rightarrow 2\left[x(tan^{-1}x)^{2}-\frac{1}{2}ln(1+x^{2}) . tan^{-1}x \right]^{1}_{0} - 2\left[\int_{0}^{1}{\frac{xtan^{-1}x}{1+x^{2}}dx} -\frac{1}{2}\int_{0}^{1}{\frac{ln(1+x^{2})}{1+x^{2}}dx}\right]
I thnk now it can be done integrate \int_{0}^{1}{\frac{xtan^{-1}x}{1+x^{2}}} by using by parts and \int_{0}^{1}{\frac{ln(1+x^{2})}{1+x^{2}}dx} can be integrated
hence i guess the question is demolished isn't it
21Are u sure u applied By parts correctly?jus check.
1
Manmay kumar Mohanty
·2010-05-01 00:45:38
yup i got my mistake and edited that [ made a mistake in 2nd step earlier ] sry [3]
but since i typed that once
once again try karne ka man nahin hai............
If my approach is correct then please tell me..............or shuld i try this in other way
21
eragon24 _Retired
·2010-05-01 01:14:05
It isnt.
check wat u did after taking ln(1+x2) = t
1
Manmay kumar Mohanty
·2010-05-01 06:40:39
sry again for a silly mistake .............but edited now.......
i thnk for that log part again we got to use by parts .
11I just wonder if this requires expansions - expansion of ln(1+x), where x=sin2θ.
21
eragon24 _Retired
·2010-05-02 03:45:12
Well i havent got this one....so cant say much.
but u all know what.....my cousin asked me this one.. day before yesterday and he says this has come in 12th board exam..
66This sum indeed came in CBSE boards two years ago. However, it was a misprint and marks were given to all who tried. This integral is not easy to be asked in the boards and the result is something like
\dfrac{\pi}{8}(\pi+4\ln 2)-2G
where G is the Catalan constant.
1
Manmay kumar Mohanty
·2010-05-02 20:38:30
but i got it as \frac{\pi }{4}\left(\pi +1 \right)-\frac{1}{2}ln2\left[\frac{\pi }{2}+1 \right]-2
@kaymant sir wuld u please elaborate a bit abt CATALAN CONSTANT. heard of it first time [7]
1Catalan's constant is a constant that commonly appears in estimates of combinatorial functions and in certain classes of sums and definite integrals
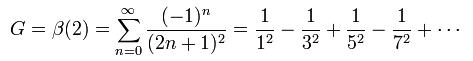
is a catalant's constant.
21
eragon24 _Retired
·2010-05-03 01:09:28
ok fine sir...
@manmay u wud hav surely be again doing some mistake thats why u r getting an anwer :P
1
Manmay kumar Mohanty
·2010-05-03 01:11:30
yes again i did
pata nahin mujhe ho kya gaya hai
11
Devil
·2010-05-03 05:24:37
Somewhere I read that this catalan const. is -\int_{0}^{1}{\frac{lnx}{1+x^2}dx}.
