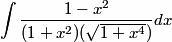1
1do one thing...
multiply upar - niche wid (1+x2) ..
so in numerator we have (1-x4)..
then divide upar-niche by x4..
this cud help...
 1
1i think a better way to do it would be as follows
we can write (1+x2)= x(1/x+x)
take (1/x+x)=t
then (-1/x2 + 1 )dx=dt
hence
(1-x2)dx = -x2dt
substituting
-x2dt/x(t)√1+x4
= -xdt/(t√1+x4)
write 1+x4 as
x2(1/x2+x2)
we get
= -dt/t√(x2+1/x2)
but we know
x2+1/x2= (x+1/x)2-2 = t2-2
after that just substitue t = √2secθ
and you will get the answer as
(θ/√2)+c
 1
1heyy this one is esay ... i din solve it in the morning.. (it was a bad method). .now i have an easier one...
mulitiply upar-niche with (1+x2).
so we have the integration as.. ∫(1-x4)dx/(1+x2)2√(1+x4)
now very carefully take out x2 from (1+x2)2 so we have x2(x+1/x)2
and take out x from √(1+x4) then we have x√(x2+1/x2) so finally wat we get is..
∫(1-x4)dx/ x3(x+1/x)2√(x2+1/x2)
= ∫(1-x4)dx/ x3(x2+1/x2 +2)√(x2+1/x2)
=∫(1/x3-x)dx/(x2+1/x2 +2)√(x2+1/x2)
now, take x2+1/x2 as t2 => -(1/x3-x) = tdt.
so the whole thing boils down to..
∫tdt / (t2-2)t
=∫dt/(t2-2)
bus! ho giya !
(the main thing is to take t= something n have the dt form of it in the numerator.. )
 1
1write d num as -(x^2+1-2)
so nw ur int bcums
-1/(1+x^4)^1/2 +2/(1+x^2|)(1+x^4)^1/2
nw put rootx as tan@
dx=2tan@sec^2@d@
so ur int bcums
2tan@sec^2@d@/(sec@) +2tan@sec^2@d@/(sec@)(sec^2@)
frost one is simply sec@tan@d@(-1) here put sec@ as t u get d answer and d second part is
sin@d@ hope u can solve this
(if ne error it may b in d constnts like 2 or 4 sumthing )