1The question is possible if it is sin4x-4
Or else the question is not possible
Answer:
∫ex(sin4x dx)/1-cos4x -∫2exdx/1-cos4x
U can write 1-cos4x as 2sin22x and sin4x as 2sin2x.cos4x
∫excot2xdx -∫exdx/sin22x
∫(excot2x dx-excosec22x)dx
now this in the form of ∫ex(f(x)+f1(x)=ex.f(x)
Now the answer is excot2x....
62dude the quesiton is possible.. but i am not sure if we have an answer at hand..
if u do it will be gr8 :)
1if 4 is given in place of 2 then we can write it as e^x(f(x)+f'(x)) where f(x)= sin4x/(1-cos 4x) :)
62This can be done if and only if we can solve
∫excot2x dx
anyone game?
1I have tried... But i believe something is wrong.. I have a strong feeling...
I think ∫excot2x dx can be done using ILATE rule... I have not tried it yet...
1i think original question was e^2x
given term= ∫e^2x(cot 2x - (cosec 2x)^2) dx
integrating by parts,
cot 2x * (e^ 2x)/2 - ∫(-2)cosec22x e2x/2 dx - ∫e^2x cosec22x.
= cot 2x * (e^ 2x)/2 +c
1I KNOW SOLUTION IS WEIRD BUT ITS 100% TRUE..............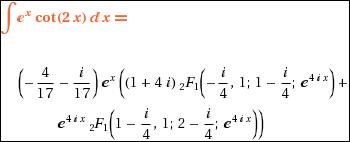
WHERE 2F1 IS HYPERGEOMETRIC FUNCTION..
REF. http://reference.wolfram.com/mathematica/ref/Hypergeometric2F1.html
