210 ...isnt it
not a doubt
I\! f \;\; 2f(x) + f(-x) = \frac{1}{x}sin(\frac{x^2-1}{x}), F\! i\! n\! d \; \; \int_{1/e}^{e}{f(x)dx}
-
UP 0 DOWN 0 0 4
4 Answers
62replace x by -x
you get a pair of simultaneous equations..
eliminate f(-x) to get f(x)
Some one finishing this off?
11As per Nishant's Sir hint :-
2 f(x) + f(-x) = 1/x sin (x - 1/x) ...................................(i)
Replace x by -x , we get
2 f (-x) + f(x) = 1/x sin (x- 1/x) ...................................(ii)
Subtracting (i) and (ii), we get
f(x) = f(-x)
Therefore, 3 f(x) = 1/x sin (x- 1/x)
Therefore, I =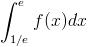 
= 1/3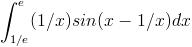 
Put 1/x = t , dx = -1/t2 dt
Therefore, I = 1/3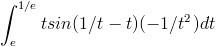 
= -1/3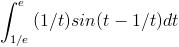 
Therefore, I = - I
2 I = 0
I = 0