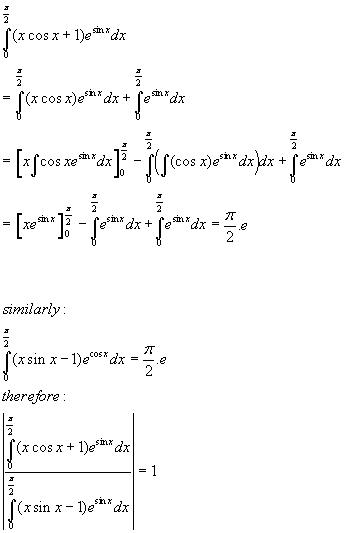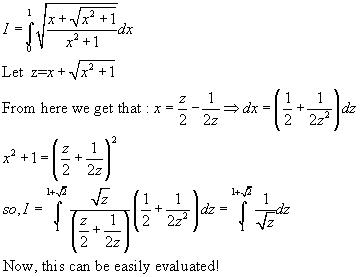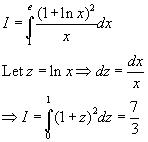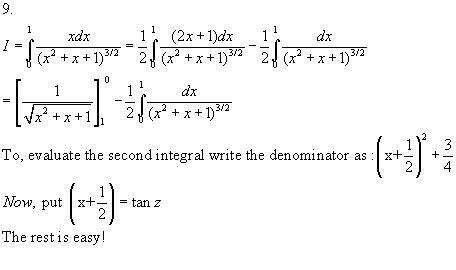ashish recheck ur solution
the answer coming out is 3
by limit as a sum
ur 2nd step is doubtful to me
this thread is only for integration sums............
AND YA FORGOT TO TELL ALL TARGETIT USERS, I HAVE COPIED ALL THESE SUMS. SO KISIKO GAALI DENA HAIN YA KUCH KEHNA HAIN, PLEASE VISIT
http://targetiit.com/profile711.html AND POST THEM IN CHATBOX. THANKS IN ADVANCE............
1}\int_{0}^{1}e^{\sqrt{e^{x}}}\ dx+2\int_{e}^{e^{\sqrt{e}}}\ln (\ln x)\ dx
2} \int \frac{x^{3}}{(x-1)^{3}(x-2)}\ dx
3}1985 japan women university
\lim_{a\rightarrow + \infty} \frac {\int_0^a \sin ^ 4 x\ dx}{a}
4} \frac{1}{\displaystyle \int _0^{\frac{\pi}{2}} \cos ^{2006}x \cdot \sin 2008 x\ dx}
5} \int_0^{\frac {\pi}{2}} \frac {x^2}{(\cos x + x\sin x)^2}\ dx
6} IF F(X)= x2 + |x| then prove that
\int_{0}^{\pi}f(\cos x)\ dx=2\int_{0}^{\frac{\pi}{2}}f(\sin x)\ dx
7}Evaluate the following definite integral.
\int_{e^{2}}^{e^{3}}\frac {\ln x\cdot\ln (x\ln x)\cdot\ln\{x\ln (x\ln x)\} + \ln x + 1}{\ln x\cdot\ln (x\ln x)}\ dx
8}
Let f a nonnegative ,continuous and periodical function defined on the reals, such that the arithmetic mean of the numbers f(1), f(2),...f(n) tends to zero when n tends to infinity. Prove that f(k)=0 for any natural number k.
9}\int_{0}^{1}\frac {x\ dx}{(x^{2} + x + 1)^{\frac {3}{2}}}
10}\int_{2}^{6}\ln\frac { - 1 + \sqrt {1 + 4x}}{2}\ dx
-
UP 0 DOWN 0 23 174

174 Answers
HAVE A LOOK AT IT
http://targetiit.com/iit_jee_forum/posts/important_information_2774.html
hey dude isko bhi integrate karo
∫ (√x-3 ) ( sin-1(ln(x) ) + cos-1(ln(x) ))
18)1.> take x=t2
the limits remain as 0 and 1
dx=2t.dt and the rest is the integral of sec-1(x)
f(x) = \int_{2}^{e^x}\frac{1}{\sqrt{\ln t}}dt
k=lnt\\ \\ t=e^{k}\\ dk=frac{1}{e^{k}}dt\\ \\ dt={e^{k}}dk\\
does this help?
hey guys do tht √1+x3 wala naa........its difficult and different........wel cubic under a root is dere for our syllabus????
HAVE A LOOK AT IT
http://targetiit.com/iit_jee_forum/posts/important_information_2774.html
The integration of √1+x3 cannot be written in terms of the elementary functions. It will come in terms of the Elliptical integral.
Q4) Ans: 2007
Hint: Write the denominator as \int_0^{\pi/2} \cos^{n-1}x \,\sin (n+1)x \ \mathrm{d}x. Exapand the sine to get:
\int_0^{\pi/2}\cos^{n-1}x \big(\sin nx \cos x + \cos nx \sin x\big)\ \mathrm{d}x\\[2ex] =\int_0^{\pi/2}\cos^nx\,\sin nx \ \mathrm{d}x + \int_0^{\pi/2}\cos nx\ \cos^{n-1}x \sin x \ \mathrm{d}x
Now integrate the second one by parts.
Bhargav.. sorry for the behavior that day..
Threads with solutions:
1) Post 26 by Manipal
2)
3) Post 8 by asish
4) Post 74 by Kamyant
5)
6) Post 7 by asish
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18) Post 29 by Manipal
19)
20)
21) Post 18 by Virang
22) Post 19 by Virang
23) Post 40 by Manipal
24) Post 27 by Tapan
25)
26) Post 12 by Akand
27) Post 16 by Akand
28)
29) Post 17 by Akand
30)
31)
32)
33)
34) Post 77 by Manipal
35)
36)
37)
38) Post 35 by Manipal
39)
40)
41)
42)
43) 55 by Asish
44) 57 by Asish
45)
46)
47)
48)
49)
50)
THANX BUDDY 4 UR KIND HELP [1]
IT WAS VERY ESSENTIAL 4 THIS THREAD
q20]
LET lnt = x2
1/tdt = 2xdx
I = ∫ex*2x/xdx
I = ∫exdx over appropriate limitsssss
First determine the indefinite integral:
I=\int\dfrac{x\cos x}{(x\sin x+\cos x)^2}\ x\sec x\ \mathrm{d}x
Note that \int\dfrac{x\cos x}{(x\sin x+\cos x)^2}\ \mathrm{d}x = \int \dfrac{\mathrm{d}(x\sin x + \cos x)}{(x\sin x+\cos x)^2}=-\dfrac{1}{x\sin x+\cos x}
Therefore,
I = x\sec x \left(-\dfrac{1}{x\sin x+\cos x}\right) + \int \dfrac{\sec x(1+x\tan x)}{x\sin x+\cos x}\ \mathrm{d}x
= \dfrac{-x\sec x}{x\sin x+\cos x} + \int \sec^2x\ \mathrm{d}x
= \dfrac{-x\sec x}{x\sin x+\cos x} + \tan x=\dfrac{\sin x-x\cos x}{x\sin x+\cos x}+C
Hence the definite integral is
\left|\dfrac{\sin x-x\cos x}{x\sin x+\cos x}\right|_0^{\pi/2}=\dfrac{2}{\pi}
We have
\mathrm{d}\big(x\ln\{x\ln(x\ln x)\}-x\big)
=\ln\{x\ln(x\ln x)\}\ \mathrm{d}x+ x \cdot \dfrac{1}{x\ln(x\ln x)}\left(\ln(x\ln x)+ x\cdot \dfrac{1}{x\ln x}\left\{\ln x+ 1\right\}\right)\ \mathrm{d}x-\mathrm{d}x
=\left(\ln\{x\ln(x\ln x)\}+\dfrac{\ln(x\ln x)+\dfrac{1+\ln x}{\ln x}}{\ln(x\ln x)}-1\right)\ \mathrm{d}x
=\dfrac{\ln x \cdot \ln(x\ln x)\cdot \ln\{x\ln(x\ln x)\}+\ln x+1}{\ln x\cdot \ln(x\ln x)}\ \mathrm{d} x
Therefore,
\int\dfrac{\ln x \cdot \ln(x\ln x)\cdot \ln\{x\ln(x\ln x)\}+\ln x+1}{\ln x\cdot \ln(x\ln x)}\ \mathrm{d} x = x\ln\{x\ln(x\ln x)\}-x +C
The definite integral can now be easily evaluated.
45.
lim n → ∞ (1/n!)^(1/n)
Since it is raised to 1/n. Here 1/∞ = 0
Therefore the ans is 1
∫ (√1+x4)dx
(1-x4 )
And haan answer in x and functions only!
Ya this sum is xeroxed one so dont be surprised if u si dis in a book !
:-D
hey dude isko bhi integrate karo
∫ (√x-3 ) ( sin-1(ln(x) ) + cos-1(ln(x) ))
@ manipal singh
dude ye to trap questoin tha ,just check ki the function exist or not[1]