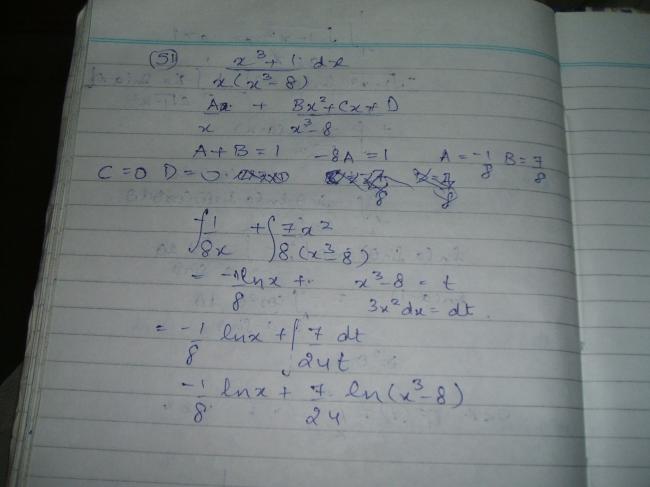161)lnx=t
1/x dx =dt
then u get a std form wich one can solve easily :P
this thread is only for integration sums............
AND YA FORGOT TO TELL ALL TARGETIT USERS, I HAVE COPIED ALL THESE SUMS. SO KISIKO GAALI DENA HAIN YA KUCH KEHNA HAIN, PLEASE VISIT
http://targetiit.com/profile711.html AND POST THEM IN CHATBOX. THANKS IN ADVANCE............
1}\int_{0}^{1}e^{\sqrt{e^{x}}}\ dx+2\int_{e}^{e^{\sqrt{e}}}\ln (\ln x)\ dx
2} \int \frac{x^{3}}{(x-1)^{3}(x-2)}\ dx
3}1985 japan women university
\lim_{a\rightarrow + \infty} \frac {\int_0^a \sin ^ 4 x\ dx}{a}
4} \frac{1}{\displaystyle \int _0^{\frac{\pi}{2}} \cos ^{2006}x \cdot \sin 2008 x\ dx}
5} \int_0^{\frac {\pi}{2}} \frac {x^2}{(\cos x + x\sin x)^2}\ dx
6} IF F(X)= x2 + |x| then prove that
\int_{0}^{\pi}f(\cos x)\ dx=2\int_{0}^{\frac{\pi}{2}}f(\sin x)\ dx
7}Evaluate the following definite integral.
\int_{e^{2}}^{e^{3}}\frac {\ln x\cdot\ln (x\ln x)\cdot\ln\{x\ln (x\ln x)\} + \ln x + 1}{\ln x\cdot\ln (x\ln x)}\ dx
8}
Let f a nonnegative ,continuous and periodical function defined on the reals, such that the arithmetic mean of the numbers f(1), f(2),...f(n) tends to zero when n tends to infinity. Prove that f(k)=0 for any natural number k.
9}\int_{0}^{1}\frac {x\ dx}{(x^{2} + x + 1)^{\frac {3}{2}}}
10}\int_{2}^{6}\ln\frac { - 1 + \sqrt {1 + 4x}}{2}\ dx
-
UP 0 DOWN 0 23 174
174 Answers
1
11QUESTION NUMBER 54
∫02 x3√1-x2dx
HERE THIS QUESTION COULD ONLY BE DONE BY SUBSTITUTING x=sinθ
OR BY PARTS BUT THERE A TERM OF sin-1x WILL COME
SO THE UPPER LIMIT WILL NOT BE DEFINED
SO ITS INTEGRAL CANNOT BE FOUND
CORRECT ME IF I AM WRONG
11QUESTION NUMBER 51
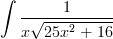
put x=4/5tanθ
dx=4/5sec2θdθ
on solving u will get
∫1/4cosecθdθ
=1/4log| cosecθ-cotθ |+C
11bhai
PLEASE NO BASHING 4 IT
30 POSTS HAVE BEEN DELETED[3][3][3][3]
11mani, even if we substitute x2=t,
we get
\frac{1}{2}\int_{0}^{4}{t\; \sqrt{1-t}\; dt}
i don't think we can do this directly so i substituted 1-t = u2
which caused a problem in the limits again (since √1-4 is complex)
1363.∫√tanx-√cotx dx
=∫√2{√sinx +√cosx}/√1-(sinx-cosx)2 dx
=∫dt/√1-t2
[taking sinx-cosx=t ]
1352.∫ dx/x√(5x)2+42
put x=1/t
dx/x2=-dt
I=-∫dt/√52+(4t)2
=-1/4ln(4t+√52+(4t)2)
substitute x
11ABHIRUP SAID IN #138
52.∫ dx/x√(5x)2+42
put x=1/t
dx/x2=-dt
I=-∫dt/√52+(4t)2
=-1/4ln(4t+√52+(4t)2)
substitute x
BHAI BOLDED SAMAJH MEIN NAHIN AAYA?????
1165. 1/a∫√1-x2dx-
1st part is by the formula....
2nd part
∫√1-x2dx/x
put 1-x2=z2
∫z2dz/(1-z2)
=-∫dz+∫dz/1-z2
=-z+1/2 ln[(1+z)/(1-z)]
substitute z
MERA BOLDED WAALA f(a+b-x) WALI PROPERTY SE NAHIN BAN RAHA
PLEASE THODA SA EXPLAIN KAR DO
11@QUESTION NUMBER 54
∫02 x3√1-x2dx
SI ISKO 0 TO 1 AND 1 TO 2 BREAK KARENGE
TO ISS MEIN 1 TO 2 WAALA INTEGRAL DEFINED NAHIN HOGA KYUNKI √1-x2
HAVE TO BE POSITIVE
SO X LIES BETWEEN -1 TO 1
IF THE UPPER LIMIT IS 1 THEN THE QUES CAN BE DONE BY PUTTING
x2=t
2xdx=dt
then
1-t=p
-dt=dp]
so by changing the limits question can be solved
SIR TILL NOW WE HAVE ONLY USD INTEGRATION TO FIND AREA IN REAL PLANE
BUT IF THIS PROBLEMS DEALS WITH ARGAND PLANE
THEN I HAVE NO PROBLEM IN SHOWING THE SOLUTION[1]
13BHAI BOLDED SAMAJH MEIN NAHIN AAYA?????
watz the problem
t=1/x
dt=-dx/x2
1\int^{\infty}_0 x / ( e^x - 1) \ dx
question 54
multiply and divide by exand then integrate u will get the answer
3976]\int {\frac{{3x^3 + 5x^2 - 7x + 9}} {{\sqrt {2x^2 + 5x + 7} }}} dx
3979] \int {\frac{{dx}} {{x\left( {2 + \sqrt[3]{{\frac{{x - 1}} {x}}}} \right)}}}