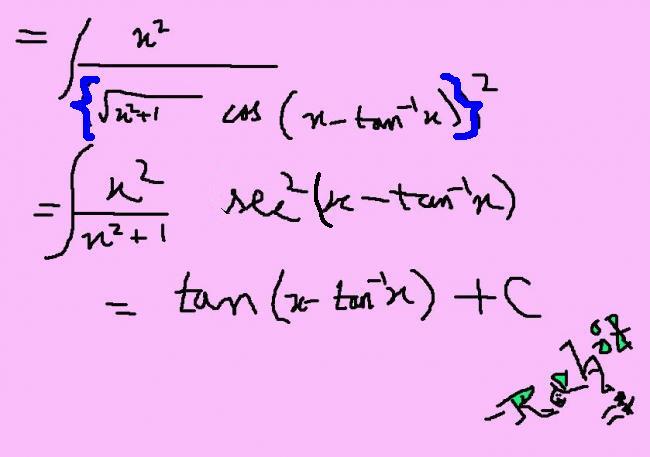i can sumwht see the solution...
I was amazed by this solution... Never saw this trick.. I hope this helps some of you...
I =\int\frac{x^{2}}{(x\sin{x}+\cos{x})^{2}}dx
Before giving the complete solution... Let me give this hint so that some of you can apply your brains and get to the answer..
Observe: x\sin x+\cos x =\sqrt{1+x^{2}}\cos (x-\tan^{-1}x)
Now try to use this to findt the integral...
This trick was posted by on another site.
-
UP 0 DOWN 0 0 9

9 Answers
SOLUTION : Put x - tan-1x = p
=>{ 1 - 1/(1+x2) }dx = dp
I = integ [ x2 / (1 +x2) cos2 (x - tan-1x) ]
= integ[ sec2p dp ]
= tan p
= (tan x - x)/ (1 + xtanx)
uttara u knw wht mah solutions is exactly the same..u just got to expand the tan part to get ur answer!!!n i think we can do that substituion of 'p' mentally uttara..:)
Btw this is not my trick ;)
Solve today's QOD based on another problem using the same trick :)