Correction in 1.
f(x)=1+x2 and f[g(x)]=1+x2-2x3+x4
Solve them quickly please---
1.If f(x)=1+x2 and f[g(x)]=1+x2-2x3+x4,then determine the function g(x) alongwith its domain and range.
2.Let f:{x,y,z}-->{a,b,c} be a one-one function.It is known that only one of teh following statement is true.
(a)f(x)≠b
(b)f(y)=b
(c)f(z)≠a
Find the function f(x),f(y)&f(z).
3.If f(x) be a function satisfying :f(x).f(1/x)=f(x)+f(1/x) and f(4)=65.
Then find f(x) and f(3).
-
UP 0 DOWN 0 0 8

8 Answers
3rd sum
f(x) luks like 1+(x)^n
f(4)=65
1+4^(n)=65
thus n =3
thus f(3)=1+3^(3)
=1+27 =28
1.
f(y) = 1 + y2
f[g(x)]=1+x2-2x3+x4
g(x) = y
y2 = x2 - 2x3 + x4
y = x2 - x4 or x4-x2
Domain is all real value but range will be different for both
2.
Lets take the first condition to be true then a) f(x)≠b then b)f(y)=b
(c)f(z)≠a is false
then possibility is:-
f(x) = a,c
f(y) = a,c
f(z) = a but since f(z) =a , f(x) = f(y) = c and therefore b is left out
Lets take the second condition to be true then a) f(y)=b then b)f(x)≠b
(c)f(z)≠a is false
then possibility is:-
f(x) = b
f(y) = b
f(z) = a but since f(z) =a , f(x) = f(y) = b and therefore c is left out
Lets take the third condition to be true then a) f(z)≠a then b)f(y)=b
(c)f(x)≠b is false
then possibility is:-
f(x) = b
f(y) = a,c
f(z) =b, c therefore the results:-
f(x)=b
f(y)=a
f(z) = c
1) g(x) is a polynimial,
say g(x)=anxn+an-1xn-1+....+a0
we have (anxn+an-1xn-1+....+a0)2= x2-2x3+x4
clearly n=2, an=±1
say g(x)=±x2+px+q
squaring and comparing, we have
g(x) either x2-x
or x-x2
domain of both functions is R, range of g1= [-1/4, ∞)
range of g2=(-∞,1/4]
3) contd..
f(4)=65
=>1±4n=65
=>±4n=64
rejecting negative sign
=>n=3
=>f(3)=1+33=28[1][1]
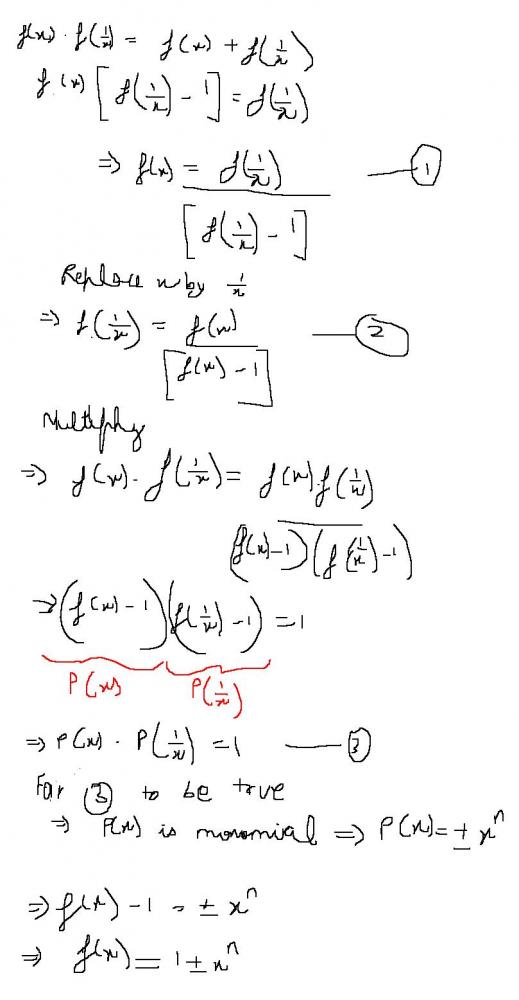 .com
.com