30We have the expansion of ln(1+x).
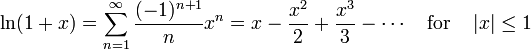
1.\lim_{x\rightarrow \infty} \frac{\left(\ln x \right)^{2}}{x} NOTE: Without L' Hospital Rule
2.\lim_{x\rightarrow \infty} \left(1+\frac{1}{x} +\frac{1}{x^{2}}\right)^{2x}
3.\lim_{x\rightarrow 1} \left(\frac{x}{x-1} -\frac{1}{\ln x}\right)
-
UP 0 DOWN 0 0 21
21 Answers
341Setting y = x-1, the given limit becomes
\lim_{y \rightarrow 0} 1 + \frac{1}{y} - \frac{1}{\ln (1+y)}
\lim_{y \rightarrow 0} 1 + \frac{1}{y} - \frac{1}{y -\frac{y^2}{2}+...}
\approx 1 + \frac{1}{y} - \frac{1}{y(1 -\frac{y}{2}+...) }
\approx 1 + \frac{1}{y} - \frac{1+\frac{y}{2}-\frac{y^2}{3}...}{y}
\approx \frac{1}{2} + \frac{y}{2}-\frac{y^2}{3}
\approx \frac{1}{2}
1i think debosmit is right ...
if you approximate ln(x)=(x-1)-(x-1)^2/2 ... u get 1/2 as limit
21sorry
3rd one kreyszig's and krishna's answer are not correct
use the series expansion of (1/1-x)
the series expansion of the given limit will be -1/lnx -x -x^2 - x^3....
hence the givn limit is zero...
1\ln(1+(x-1))=(x-1)-\frac{(x-1)^2}{2}+\frac{(x-1)^3}{3}+...\infty \\ \texttt{Hence as x tends to ln(x) tends to (x-1)} \\ \lim_{x\rightarrow 1}\frac{x}{x-1}-\frac{1}{\ln(x)}= \lim_{x\rightarrow 1}\frac{x-1}{x-1}=1
21Alt for 1
Let lnx = t
it becomes t2/et with t→∞
use expansion of e^x
1\lim_{x\rightarrow \infty}\left(1+\frac{1}{x}+\frac{1}{x^2} \right)^{2x}=e^{\ln\left( \lim_{x\rightarrow \infty}\left(1+\frac{1}{x}+\frac{1}{x^2} \right)^{2x}\right)} \\ \\ = e^{\lim_{x\rightarrow \infty}2x \ln\left( \left(1+\frac{1}{x}+\frac{1}{x^2} \right)\right)} \\ \\ \texttt{apply ln(1+y) expansion ,put y=}\frac{1}{x}+\frac{1}{x^2} \texttt{ and take limit } \\ \texttt{Ans.=}e^2
1its coming....
xlnx-x+1/(x-1)lnx
in the numerator add and subtract lnx,u`ll get....
1 +[lnx-x+1/(x-1)lnx)]....now apply expansion....
ln(1+x-1) is
(x-1) - (x-1)2/2 + (x-1)3/3 - ...........
(x-1) will get cancelled....then divide the numerator and denominator by (x-1) 2 times and then put the limit........
12. lt x\rightarrow∞ (1+1/x2+ 1/x)2x
put the limits....the expression within the brackets is exactly equal to 1....so the answer will be....
(1)∞=1
30Sorry.. sorry.. I forgot to mention, you have to solve the 1st one without L' Hospital rule.
30Well, I did get the answer to 2 as e2, but that was by another method!. Is it what you're getting too?
12. multiply and divide by (1-1/x)2x....the numerator will come in the form of (1-1/x3)2x and the denominator (1-1/x)2x....now try
30Debosmit I'm not too sure abt your resoning.. The thing inside the bracket is not exactly equal to 1 but close to one, and subquently leads to an intedeterminate form on raising it to the power of infinity.
In that case, \lim_{x\rightarrow \infty}\left(1+\frac{1}{x} \right)^{x} should be 1 too. But we know, the limit is e.