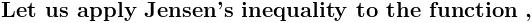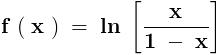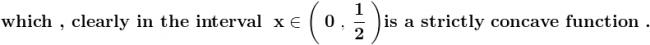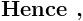I am starting a thread after a long time - hope everyone participates [1][4]
2 > 
= ??????
212) r u sure that this doesnt involve any hi level concept
from wat i hav learnt recently this is a double reimann sum for f(x,y)=\frac{x+y}{x^{2}+y^{2}}
so we hav to compute this \int_{0}^{1}{\int_{0}^{1}{\frac{x+y}{x^{2}+y^{2}}\,dx}\,dy}
isnt it? or i m rong?
but this isnt in syllab !
and is teh ans pi/2 +ln2
21its infact Stolz–Cesà ro theorem-
http://en.wikipedia.org/wiki/Stolz%E2%80%93Ces%C3%A0ro_theorem
seen this one used somewer...dun rem wer.
21if i cud get it properly
\fn_cm \\a_{n}: =\sum_{i = 1}^{n}\sum_{j = 1}^{n}\frac{i+j}{i^{2}+j^{2}},\\\\ b_{n}: = n\qquad\forall n\in\mathbb{N}.\\ \begin{align*}\ell_{n}:=\frac{a_{n+1}-a_{n}}{b_{n+1}-b_{n}}& = \sum_{i = 1}^{n+1}\sum_{j = 1}^{n+1}\frac{i+j}{i^{2}+j^{2}}-\sum_{i = 1}^{n}\sum_{j = 1}^{n}\frac{i+j}{i^{2}+j^{2}}\\ & =\sum_{i = 1}^{n+1}\frac{i+(n+1)}{i^{2}+(n+1)^{2}}+\sum_{j = 1}^{n+1}\frac{(n+1)+j}{(n+1)^{2}+j^{2}}\\ & = 2\sum_{i = 1}^{n+1}\frac{i+(n+1)}{i^{2}+(n+1)^{2}}.\end{align*} \ \\
\fn_cm \\\textup{from Stolz–Cesà ro theorem} \lim_{n\rightarrow \infty}\frac{a_n}{b_n}=\lim_{n\rightarrow \infty}\frac{a_{n+1}-a_{n}}{b_{n+1}-b_{n}}=k \\ so
\fn_cm \\ k= 2\lim_{n\to\infty}\frac{1}{n+1}\sum_{i = 1}^{n+1}\frac{\frac{i}{n+1}+1}{\left (\frac{i}{n+1}\right )^{2}+1}\\ & = 2\cdot\int_{0}^{1}\frac{x+1}{x^{2}+1}\,\mathrm{d}x\\ & =\frac{\pi}{2}+\ln (2).
i guess this was wat gallardo wanted or not :P
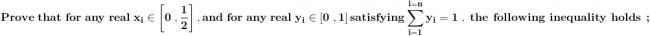
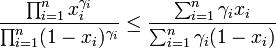
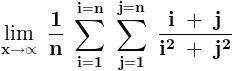