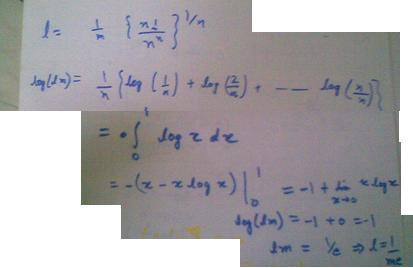is the answer 1/m...?
15 Answers
lim 1/m [n.(n-1).(n-2)... 1 / n^n]^1/n
n→∞
1/m . lim [1.(1-1/n).(1-2/n)...(1-n/n)]^1/n
n→∞
now, let k = lim [1.(1-1/n).(1-2/n)... (1-n/n)]^1/n
n→∞
=> log k = lim 1/n [ log 1 + log(1-1/n) + log(1-2/n) + ... log(1-n/n)]
n→∞
now as x --> 0 , logx --> -∞ and as n→∞ ... log k ~ -1
=> k = e^-1
=> ans is k/m = 1/em....
{well, i'm not sure whether the procedure is mathematically approvable or not... [6]sorry if it's wrong... [2] }
i think there is some problem with ur soln MAQ
I will try to post my own...
yes bro... wid pleasure... i know dat i'm wrong... my solution is answer oriented one... [4]
u better post d correct solution... [1]
Yet, there isnt any conceptual mistake, i think!
U have just cancelled off n and nn, right????
nope... i've divided each n evry term of n! wid n... so 'n' terms are divided by 'n' n's...!!!
dat is not d mistake... d mistake is in my interpretation of d limit as -1... i think dat interpretation is not completely correct...!!!
okk...... n actually i didnt think much abt ur interpretation of the limit as -1......
now as x --> 0 , logx --> -∞ and as n→∞ ... log k ~ -1
=> k = e^-1
=> ans is k/m = 1/em....
{well, i'm not sure whether the procedure is mathematically approvable or not... sorry if it's wrong... }
The solution follows...
btw scan pe mat jao..