almost every irratinl pe discont. hogi.......

g(x)= x2 , if x is rationaal
= 0 if x is irrational
then
1.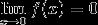
2.
3.
4.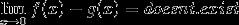
-
UP 0 DOWN 0 0 20

20 Answers
Actually YA!! mayb i found out Y ot the mathematical reason though........
it goes lyk this :
As the transition between a rational & an irratnal as infinitesimally small,
Eg. 3.999999999999999999999999999999999 wich is still rational (remembering dat v consider den as a Co-Prime of Num ) of the type 3999999999999999999999999999999999/ 1000000000000000000000000000
and bcums irratnal only wen 3.999999999........ ∞ times
so the number in BOLD tends to infinity as v undergo a transition frm rational to irratnal.....
and hence 1/Q wer Q----> ∞ is "0" and hence it is continous as its immediate next value wich is an irrrational and the functn is "0"
Any nno. x is of the form P/√Q
Let Q + h = t2 ............ lim h--->0
now at x of the form p/√Q, f(Q) = 0 .......... parametrised
and f(Q + h) = 1/t
.
.
....
.......
OH [11]
okay!!
lemme try........
iska matlab I gotta Prove 1/q ---> 0 as x tends to IRRational.........
On the contrary tapan, this function (#11) is continuous for all irrational numbers. It will be a nice exercise if you could prove this.
f(x)=1/q if x is rational and x=p/q (p,q coprime)
f(x)=0 if x is irrational
discuss the continuity of this function ...
Yes 1 2 3 are rite
F(x) = √x2 + x3
Therefore if f(0) = 0
Therefore 1 is true
G(x) = x2
G(0) = 0
Hence 2 is true
Let P(x) = F(x) - G(x)
P(x) = x2 + x3 - x2
P(0) = 0
Therefore 3 is true and 4 is wrong
bhaiyya.........
wasn't this too simple or is there sth that i'm not noticing??
lol..
i will post the question too. :P (after strainning my eyes a bit i was able to understand it :P)
f(x)=\sqrt{x^2+x^3}
g(x)=x^{2} if x is ratinal
= 0 if x is irratinal..
then
\\1) \lim_{x\rightarrow 0} f(x) =0 \\ 2) \lim_{x\rightarrow 0} g(x) =0 \\ 3) \lim_{x\rightarrow 0} (f(x)-g(x) =0 \\ 3) \lim_{x\rightarrow 0} (f(x)-g(x) =\text{does not exists!} \\