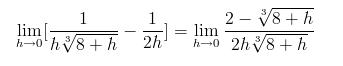1i think it should be cos2x in the first question .....
1)\lim_{x\rightarrow 0}\frac{sin(\pi cos^2 \pi)}{x^2}
Î (pi)
2)lim x→1(1+cos \pi x)cot^2 \pi x
1/2
3)\lim_{h\rightarrow 0}[\frac{1}{h^3\sqrt{8+h}}-\frac{1}{2h}]
-1/48
4)\lim_{h\rightarrow 0}\left[\frac{(a+h)^2sin(a+h)-a^2sina}{h} \right]
a^2cosa+2asina
5)\lim_{n\rightarrow \propto } cos(x/2)cos(x/4)cos(x/8)........cos(x/2^n)
sinx/x
6)\lim_{x\rightarrow \pi/2}tanx\log_{e} sinx
0
7)\lim_{x\rightarrow \propto }\frac{3^{x+1}-5^{x+1}}{3^x-5^x}
5
some more doubts left [3][3][3][3][3][3]
-
UP 0 DOWN 0 0 13
13 Answers
29In the first question just use the L'hospital rule..
\lim_{x\rightarrow 0}\frac{sin(\pi cos^2 x)}{x^2} = \lim_{x\rightarrow 0} \frac{cos(\pi cos^{2}x)(-)2xsinxcosx}{2x}
\lim_{x\rightarrow 0} \frac{cos(\pi cos^{2}x)(-)2\pi xsinxcosx}{2x} = \lim_{x\rightarrow 0}{-\pi cos(\pi cos^{2}x)} * \lim_{x\rightarrow 0}\frac{sinx}{x}
1use lhospitals rule for first and 6th ul get the answer as Î and 0...
1for the 5th ques multiply and divide it with 2nsinx2n ... then use
2sinx cosx=sin2x it will get converted to sinx2nsinx2n .. then just use limit x tends to 0 sinxx=1 ...
1for 4th ques also use lhospitals rule ... diff the num and denominator w.r.t h ul get the ans
1for the second question use 1+cosx=2sin2x2 in the numerator and in the denominator write sinx as 2sinx2cosx2 .. u will be left with
limit x tends to 1 cos2Î x2sin2Î x2 which is 12 ....
14th question
differentiating the numerator using product rule you will get
[2(a+h)sin(a+h)]+[(a+h)2cos(a+h)] and differentiation of denominator is 1 now put h=0 in the numerator that gives the answer
very simple :)
66For the 4th one, notice that the given expression is simply the definition of derivative of the function f(a)=a2 sin a w.r.t a.
And so the required result is a2 cos a + 2a sin a.
29Ans 7 lim_{x\rightarrow \propto }\frac{3^{x+1}-5^{x+1}}{3^x-5^x} = lim_{x\rightarrow \propto } \frac{5^{x+1 }([\frac{3}{5}]^{x+1}-1) }{5^{x}([\frac{3}{5}]^{x}-1)} = 5
if 0≤n≤1 then n∞ = 0
Ans 3...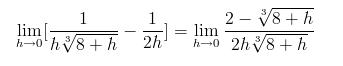
Now use L'Hospital rule