@ Avik bhai....thats not the answer :(
Q1)
For any acute angled triangle, \Delta ABC find the minimum value of
\frac{sin A}{A}+\frac{sin B}{B}+\frac{sin C}{C}
Q2) Find the volume of the largest cylinder that can be inscribed in a sphere of radius 'r' cm.
Q3) A cone is made from a circular sheet of radius \sqrt{3} by cutting out a sector and keeping the edges of the remaining pieces together. Then find the maximum volume attainable for the cone.
Q4) Suppose velocity of waves of wavelength\lambda in the Indian ocean is k\sqrt{\left\{\left(\frac{\lambda }{a} \right)+\left(\frac{a}{\lambda } \right) \right\}}
where k and a are constants. Show that minimum velocity attained by the waves is independent of constant a.
-
UP 0 DOWN 0 1 9

9 Answers
Apart from Q1, the others seem like NCERT Class XII problems...I'll do Q2 to demonstrate.
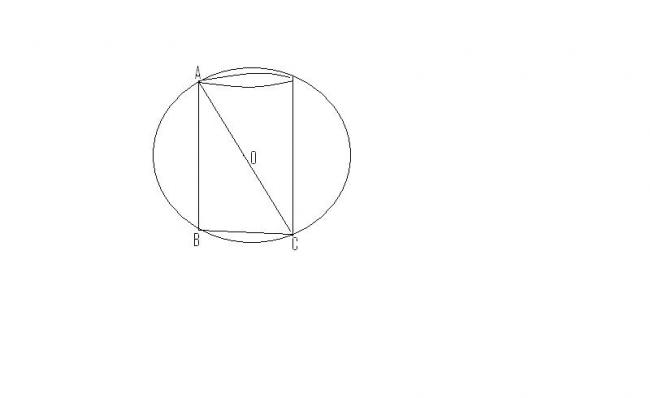
Let the radius of the sphere be r.
The radius and height of the cylinder whose volume is to be maximised are R and H.
From the triangle ABC, we have the relation -
H² + 4R² = 4r²
=> R² = (2r - H)(2r + H)/4
Now the volume of the cylinder is :
V = pi R² H
= pi (4r² - H²)H/4
= pi r²H - H3/4
Now V is a function of H, as r is not changing.
So apply the first and double derivative tests to check for points of maxima, and then find the maximum value.
PS : I might have done a silly mistake in calculations here..
These are not my doubts[1]
Thanx...can u post the final answer to ur solution?
Answers
1) \frac{9\sqrt{3}}{2\pi }
2) \frac{4\pi r^{3}}{3\sqrt{3}}
3) \frac{2\pi }{3}
Yeah, fr Q1) keep the angles as 600 each. (This is a shortcut)
Trying out fr a method frm inequalities though [1]
The following theorem is needed to these type of problems swiftly and with accuracy - - - -
Jensen ' s Inequality -
If a function f ( x ) is convex in a given interval ( a , b ) ; i . e , its double derivative is negative in that interval , then the following inequality holds -
f ( x1 + x2 + x3 + ...... xnn ) ≤ f ( x1 ) + f ( x2 ) + f ( x3 ) + ...... + f ( xn )n
for real points x1 , x2 , x3 in the function ' s domain belonging to ( a , b ) .
If the function is concave in that interval , then the inequality sign reverses .
In this case , take f ( x ) = sin xx in the interval ( 0 , Î 2 ] .
Clearly , f ( x ) is convex in the said interval .
So apply Jensen's inequality .
f ( A + B + C3 ) ≤ f ( A ) + f ( B ) + f ( C )3 , where A , B , C are the angles of the triangle .
Or , f ( Π/ 3 ) ≤ ............
Or , [ sin ( Π/ 3 )Π/ 3 ] x 3 ≤ sin AA + sin BB + sin CC
or , 9 √ 32 Π≤ sin AA + sin BB + sin CC