May be easy....

I am unable to see the latex output. Also unabel to latex. Any settings problem?

f(x) is a continuous function, which is twice differentiable - function is from Reals to Reals.
Given |f(x)|≤1 & |f"(x)|≤1, inequality for both holds true for all real x.
Prove |f'(x)|<2, for all real x.

Dude that was a good question, heres wat I have to say...

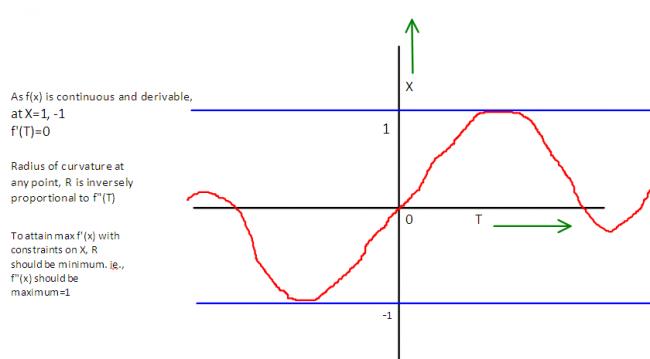
Now assuming the function to be the equation of motion of a particle moving on a straight line........

x=f(t)
v=f'(t)
a=f"(t)
As a limiting case, to attain max velocity within a given distance acceleration should be maximum....a=±1

Now say at some time t=t_o, the object is at x=1 and started at x=0 at time t=0, this can be attained by moving the Y axis, ie.,changing the time of start of observation.

Also the object has max velocity at x=0, and min acceleration=-1 during this part of motion

NOTE
if the object has max velocity at x<0, it wont be able to attain f'(T)=0 at x=-1
and if the object has max velocity at x>0, it wont be able to attain f'(T)=0 at x=1

So it is only possible at x=0

As v=0 at x=-1, or t=t_o
Using, v=u+at {acceleration is constt during this period of motion, laws applicable}
0=u-t_o
u=t_o, numerically
Using s=ut +at²/2

1=u²-u²/2 =u²/2

Hence, u=±√2

Minimum velocity is obtained at x=0 using a=1, during motion from t=0 to t=t_o, x=-1 when t=t_o, as -√2

So velocity lies in [-√2,√2]

|u|≤√2

=> |f'(t)|≤√2<2

So in the given problem, |f'(x)|<2

Solved for a good long tym to achieve this, please let me know NE errors in the solution

[339]