Nice Integral-~~~~

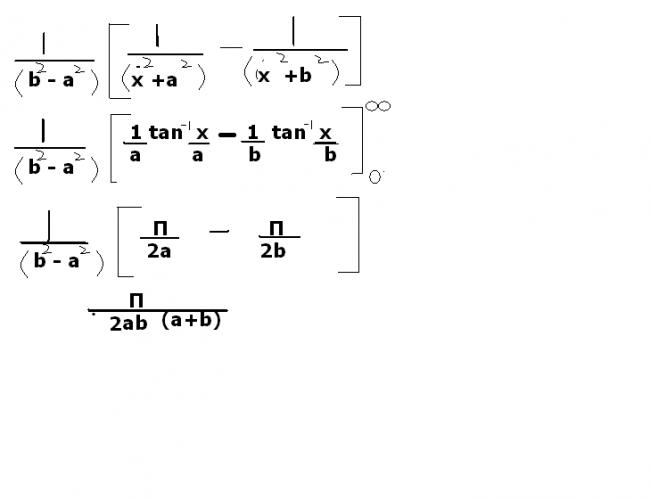
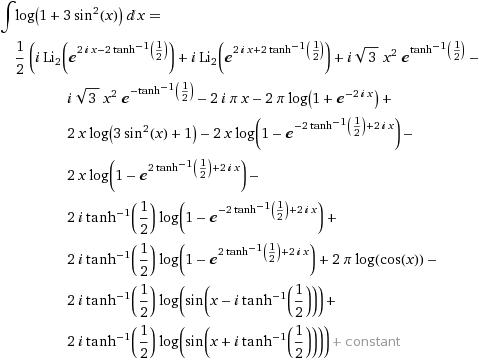I=\int_{0}^{1}{\frac{x^{a-1}-x^{-a}}{(1+x)lnx}dx} \\=\int_{0}^{1}{\frac{x^{a-1}}{(1+x)lnx}dx}-\int_{0}^{1}{\frac{x^{-a}}{(1+x)lnx}dx} \\ \\Substitute\: x=\frac{1}{t} \: in\: second\: integral \\we\: get: \\=\int_{0}^{1}{\frac{x^{a-1}}{(1+x)lnx}dx}+\int_{1}^{\infty}{\frac{t^{a-1}}{(1+t)lnt}dt} \\=\int_{0}^{\infty}{\frac{x^{a-1}}{(1+x)lnx}dx} \\Consider:\: f(a)=\int_{0}^{\infty}{\frac{x^{a-1}}{(1+x)lnx}dx} \\\frac{\partial f}{\partial a}=\int_{0}^{\infty} {\frac{x^{a-1}}{1+x}dx} \\Now\: substitute\: x=\frac{1}{z}-1 \\You\: will\: get: \\\frac{\partial f}{\partial a}= \int_{0}^{1}{z^{-a}(1-z)^{1-a}}=\beta(1-a,a)=\pi cosec(a\pi) \\f(a)=-ln\left|cosec\pi a+cot\pi a \right|+c \\f\left(\frac{1}{2} \right)=0 \\or,\: c-ln\left|cosec\frac{\pi}{2} +cot\frac{\pi}{2} \right|=0 \\or,\: c=0 \\Therefore: \: I=-ln\left|cosec\pi a+cot\pi a \right|

Beta function is not in JEE syllabus. I have used a property of beta function in my solution only because I was not able to evaluate the integral in any other way.

Do point out any mistake in my solution.

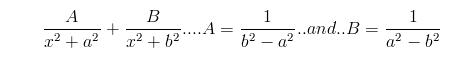
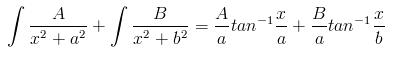Consider integrating \,\phi(\alpha)=\int_0^\pi\,\ln(1-2\alpha\cos(x)+\alpha^2)\;dx\,
now,
\begin{align} \frac{d}{d\alpha}\,\phi(\alpha)\, &=\int_0^\pi \frac{-2\cos(x)+2\alpha}{1-2\alpha \cos(x)+\alpha^2}\;dx\, \\ &=\frac{1}{\alpha}\int_0^\pi\,\left(1-\frac{(1-\alpha)^2}{1-2\alpha \cos(x)+\alpha^2}\,\right)\,dx\, \\ &=\frac{\pi}{\alpha}-\frac{2}{\alpha}\left\{\,\arctan\left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,\right\}\,\bigg|_0^\pi. \end{align}
As x varies from 0 to \pi, \left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,varies through positive values from 0 to infinity when -1<\alpha <1 and \left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\, varies through negative values from 0 , -\infty when \alpha < -1,or,\alpha >1
Hence,
\\arctan\left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,\bigg|_0^\pi=\frac{\pi}{2}\, when -1<\alpha <1
\\arctan\left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,\bigg|_0^\pi=-\frac{\pi}{2}\, when \alpha < -1,or,\alpha >1
Therefore ,
\frac{d}{d\alpha}\,\phi(\alpha)\,=0\, when -1<\alpha <1
\frac{d}{d\alpha}\,\phi(\alpha)\,=\frac{2\pi}{\alpha}\, when \alpha < -1,or,\alpha >1
Upon integrating both sides with respect to wrt \alpha we get \phi (\alpha ) = C_{1} when -1<\alpha <1

and \phi (\alpha ) = 2\pi ln\left|\alpha \right|+C_{2} when \alpha < -1,or,\alpha >1
C₁ can be determined by setting \alpha = 0

we get C₁ = 0
to determine C₂ we substitute http://latex.codecogs.com/gif.latex?\alpha%20=\frac{1}{\beta%20} where -1<\beta <1
\begin{align} \phi(\alpha) &=\int_0^\pi\left(\ln(1-2\beta \cos(x)+\beta^2)-2\ln|\beta|\right)\;dx\, \\ &=0-2\pi\ln|\beta|\, \\ &=2\pi\ln|\alpha|\, \end{align}
hence we can conclude \phi (\alpha ) = 0,-1<\alpha <1 and
\phi (\alpha ) = 2\pi ln\left|\alpha \right| when,-1>\alpha ,\alpha >1

@soumik
I was wondering how you got that integral in the second step in terms of cos inverse.

Are these things at all are reqd?

I(k)=\int_{0}^{\pi}{ln(k+cos\alpha)d\alpha}

I'(k)=\int_{0}^{\pi}{\frac{d\alpha}{k+cos\alpha}}=\frac{1}{\sqrt{k^2-1}}\left\{cos^{-1}\left(\frac{k+1}{k+1} \right)-cos^{-1}\left(\frac{1-k}{k-1} \right) \right\}

From which we get

I'(k)=\frac{-\pi}{\sqrt{k^2-1}}

I(k)=-\pi ln|k+\sqrt{k^2-1}|+c

For figuring out the const. we have for k=1, I(1)=2\int_{0}^{\frac{\pi}{2}}{ln(sin\alpha) d\alpha}=2\pi ln \left(\frac{1}{2} \right)

Thus the const. c=2\pi ln\left(\frac{1}{2} \right), and we need I\left(\frac{10}{6} \right).

Many might be wondering what the heck I\left(\frac{10}{6} \right) - let me clear that.

See ln(10+6cos\alpha)=ln6\left(\frac{10}{6}+cos\alpha \right)=ln6+ln\left(\frac{10}{6}+cos\alpha \right).....

Finally plugging the values, we have the ans as \boxed{I=2\pi ln3} - as said by kaymant sir.

Done!!! [56]

sir i meant the bracket in second last line is closed after the integration is performed
sorry for that
actually these latex symbols made me so confused about placing
i hope its correct now

For 2) use the following general result:

\int_0^\pi \ln(1-2a\cos x+a^2)\ \mathrm dx =\left\{\begin{matrix} 0 & \text{ if } |a|\le 1\\[2ex] 2\pi\ln |a| & \text{ if } |a|>1 \end{matrix}}\right.
to get the required result as 2\pi \ln 3

substitute

P.S use of mathematica shud be avoided

@Tapas..can u plz explain ur method..

2 can be broken into integral of (below) and 2log2 parts;

no thats not a typo