\hspace{-16}\bf{(1)\;\;}$ Total no. of real solution in $\bf{2^x = x^2}$\\\\\\ $\bf{(2)\;\;}$ Total no. of real solution in $\bf{2^x = 1+x^2}$\\\\\\ $\bf{(3)\;\;}$ Total no. of real solution in $\bf{2^x+3^x+4^x+5^x = 10x+4}$\\\\\\
-
UP 0 DOWN 0 1 1

1 Answers
The first 2 questions have 3 solutions each.
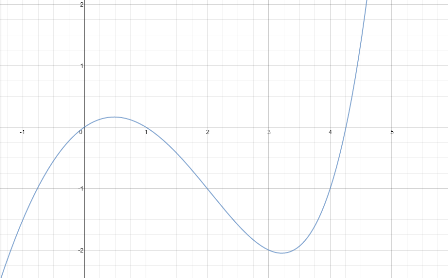
For number 2.
\text{Consider }y=2^x-x^2-1
By hit and trial we can find 2 solutions for y=0 .
x=0 and x=1.
\lim_{x\rightarrow \infty}y = \infty
\text{and }\lim_{x\rightarrow -\infty}y = -\infty
But if there were 2 solutions the graph for y vs x would change sign only twice and the sign of both the limits would have been the same.But they are opposite in sign.So there must another root.Using this logic I guess we can conclude that there are 3 roots for y=0.
Similarly question 1 can be solved.
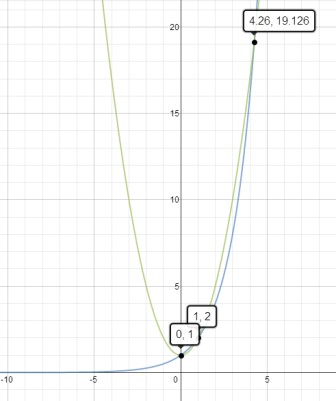
Graph of 2x and x2+1:
Graph of y = 2x-1-x2: