146drawing the graph i am getting option c for the q. 83
shivendu gupta given answer is d.
6 Answers
1357The graph will look like this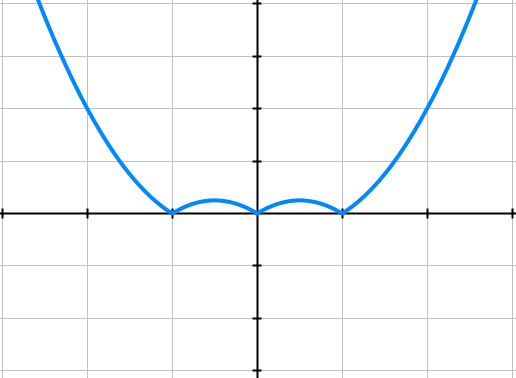
Which shows it has 5 critical point
- shivendu gupta thank you vey much.Upvote·0· Reply ·2014-08-13 09:23:23
146146for q. 89 ans is option 2
- shivendu gupta given answer is d here too.
46684 .(2)
- Himanshu Giria Where are the other options for85??
- Himanshu Giria 86 is marked correct as4
- Himanshu Giria Sorry88not86
- shivendu gupta this is correct,wil you please tell me how to solve?
- shivendu gupta for ques. 85 options are :
(c) 3a-b>o,d=3a+2b
(d) none
466In 90 i guess α can have any real value so I guess all the4options are correct
...
- shivendu gupta given ans. is 3
Sahil Jain alpha cannot be negative since if its is negative the funtion becomes logx/x which is not defined at x = o. So contradictory results appear
1708\hspace{-16}$For $\bf{(85)::}$ Given $\bf{ax^3+bx^2+cx+d = a(x-1)^2\cdot (x-\gamma).........(1)}$\\\\\\ Where $\bf{a>0}$ and $\bf{\gamma<0}$, Now put $\bf{x=1}$ on both side, we get\\\\\\ $\bf{\Rightarrow a+b+c+d = 0\Rightarrow c=-\left(a+b+d\right)}$\\\\\\ Now Diif. equation $\bf{(1)}$ both side w. r to $\bf{x\;,}$ we get\\\\\\ $\bf{\Rightarrow 3ax^2+2bx+c = a\left\{(x-1)^2+2(x-1)(x-\gamma)\right\}}$\\\\\\ Now put $\bf{x=1}$ on both side, we get\\\\\\ $\bf{\Rightarrow 3a+2b+c = 0\Rightarrow 3a+2b-a-b-d = 0\Rightarrow \boxed{\boxed{\bf{2a+b=d}}}}$\\\\\\ (Using $\bf{c=-\left(a+b+d\right)}$)\\\\\\ Now Using Product of Roots for equation $\bf{(1)\;,}$ We get\\\\\\ $\bf{\Rightarrow \gamma = -\frac{d}{a}\Rightarrow d=-\gamma \cdot a >0}$\\\\\\ So $\bf{d=2a+b>0}$\\\\\\ So $\bf{\boxed{\boxed{\bf{d+a= 2a+b+b>0\Rightarrow 3a+b>0}}}}$\\\\\\ bcz $\bf{a\;,d >0}$