11
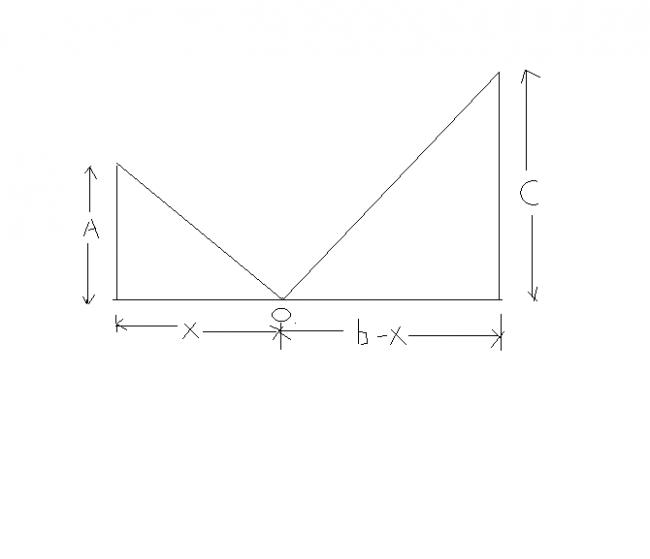
let the man travel with speed v and let him touch the wall at o
total distance covered (D)= √(a2+x2) + √((b-x)2+c2)
total time taken by him would be = D/v....(1)
time taken by man would be least if he travels the least distance,therefore
differentiate(1)wrt to x to get the value of x corresponding to least time
341This is a popular example to demonstrate how you can obtain minimum without using calculus:
Reflect the point Q across the wall so that now P and Q are on the opposite sides of the wall. Let the reflected point be Q' and O the point of intersection of PQ' and the wall.
Now consider any other point O' on the wall.
Its easy to see that PO' + O'Q = PO' + O'Q'
By triangle inequality, PO' + O'Q' > PQ'.
So to minimise the distance travelled, you must first go to the point O which is the intersection of wall and PQ'.
From simple geometry, the two angles are equal, so the equation is simply
\frac{x}{a} = \frac{b-x}{c}
24yeah sir ..this is the best and quickest methood to reach the answer..[1][1]
341
Hari Shankar
·2009-07-14 08:36:18
If you know inequalities, this is the Minkowski inequality at work.
\sqrt{x^2+a^2} + \sqrt{(b-x)^2 + c^2} \ge \sqrt{b^2 + (a+c)^2} with equality when \frac{x}{b-x} = \frac{a}{c}