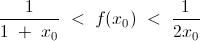71Let us define another function " g ( x ) " as :
How do I know which function to define. You took the second expression of g(s) as tan-1 x . How?
1) Evaluate the limit: \lim_{n\to\infty} |\sin (\pi\sqrt{n^2+n+1})|
2) Prove that
\lim_{n\to \infty}n^2 \int_0^{1/n} x^{x+1}\ \mathrm dx=\dfrac{1}{2}
3) Find the real parameters m and n such that the graph of the function f(x) = (8x3 +mx2)1/3 - nx has the horizontal asymptote y = 1.
4) Let f:[0,1]→R be a continuous function with the property that
\int_0^1 f(x)\ \mathrm dx = \pi/4
Prove that there exists x0 in (0,1) such that
\frac{1}{1+x_0}<f(x_0)<\frac{1}{2x_0}
-
UP 0 DOWN 0 0 19
19 Answers
71
1Seoni , your mistakes are : -
1 . See the first mathematical expression Anant Sir has written : -
| sin ( nπ + θ ) | = | sin θ |
If " n " is not an integer , could you write that ?
2 . We do not want " n " to be an integer , but an even or odd multiple of " 12 " , which can easily happen .
My solution : - We see that , for a very large " n " , we have : -
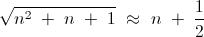
So , for " n → ∞ " , we must have : -
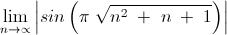
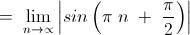
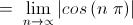
Now , as " n " tends to infinity along integer points , we see that the given limit tends to 1 .
But , if it does not do so , then the limit doesn't exist .
1sir
why do u say
'And when n approaches infinity by taking integral values,'
1]wont d above expression in bracket approach 1/2 irrespective of
n being integer/ non integer....? so limit=1,,,
2]but looking at initial expressiion,
root n2+n+1 can't be perf square, so even if n is integer, root n2+n+1 can't be an integer...so limit'll oscillate...
which out of 1] & 2] is right,
66@Vivek, it won't be oscillating. The reason is the presence of the modulus. First of all,
|sin(nπ+θ)|=|sinθ|
Secondly, the square in n cancels out in the numerator. So after your last step, we get
=\lim_{n\to\infty} \left|\sin\left(\dfrac{n+1}{n+\sqrt{n^2+n+1}}\,\pi\right)\right|
And when n approaches infinity by taking integral values, we get the limit as |sin(Ï€/2)|=1
71If I try a bit mathematical approach for the first sum :
We have \lim_{n\to\infty} |\sin (\pi\sqrt{n^2+n+1})|
= \lim_{n\to\infty}|\sin(2n\pi - \pi\sqrt{n^2+n+1})|
= \lim_{n\to\infty}|\sin(n\pi + n\pi - \pi\sqrt{n^2+n+1})|
= \lim_{n\to\infty}|\sin(n\pi+ \frac{(n\pi)^{2}-(\pi\sqrt{n^2+n+1})^{2}}{n\pi+\pi\sqrt{n^2+n+1}} )|
= ...
However at the last step we have oscillating limit and hence the limit won't exist! (I think)
Please Correct me Ricky Bhaiya and Kaymant Sir!
1Sir , the answer to the first problem depends upon " n " as far as I can think . If " n " approaches infinity being an integer all along , then the answer should be " 1 " . However , for any general " n " , I don't think the limit exists Sir .
1@vivek sure i will tell u what ricky told me regarding deciding the function
first para from my side
There is no rule for defining function......infinitely many tips can be given regarding that and they can fail infinte times if u proceed that way..the hint for function "sometimes" i mean only "sometimes" is "directly" given in problem...most of the time it is our imagination(like the way we do in integrations :P) which helps us find the function!
second para is what ricky told me:
basic rule:a function satisfying condition of the problem and Rolle's or LMVT(as the case may be)..which may after some manipulations give the required expression to be proved!
1and is this standard limit in jee syllabus?...i got stuck at the final step because of being unable to evaluate it!
1Let us denote the given limit by " L " . Now , if we do the following substitution : -
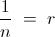
We find immediately that , the given limit is in - fact : -
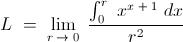
( Now applying L - Hospital ' s Rule along with Newton - Liebniz Lemma , we obtain : - )
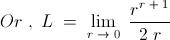
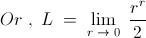
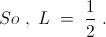
The proof of the standard limit ,
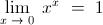
can be found here : -
http://math.depaul.edu/mash/limitofx%5Ex%5E.pdf
1Let us define another function " g ( x ) " as : -
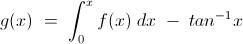
It is easy enough to see that : -
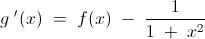
Now , " g ( 0 ) = g ( 1 ) = 0 " .
So , " g " satisfies all the conditions of Rolle's theorem in the interval " ( 0 , 1 ) " .
So , for some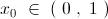 
, we must have : -
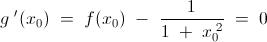
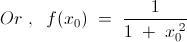
Here , we can obtain an inequality as : -
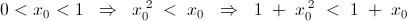
We also have : -
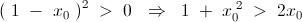
These two inequalities together give us : -
