prove

AIEEE Answers › Calculus questions › prove

prove that
2\pi <sin xx<1

for x e (0,\pi 2)

#Mathematics #Calculus

UP 0 DOWN 0 0 6
Post on FacebookPost anonymously?

6 Answers

11

Tush Watts ·2009-11-20 21:30:42

Ans) Let f(x) = sinxx
Since f(x) is dec in the interval (0 , âˆ©/2)

Therefore, f(0) > f(x) > f (âˆ©/2)
That implies, 1 > sinxx > 1âˆ©/2 = 2 / âˆ©

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Kaustab Sarkar ·2009-11-20 22:53:00

ths toh i know

but how to prove that f'(X)<0 for proving it to be dec func

how to prove that (xcosx-sinx)/x² is <0

UP 0 DOWN 0
Post on FacebookPost anonymously?

24

eureka123 ·2009-11-20 23:37:02

x²>0 for x>0
so only thing left to prove is xcosx-sinx<0

which is true iff sinx>xcosx
=> tanx>x

which is true ...(See graph)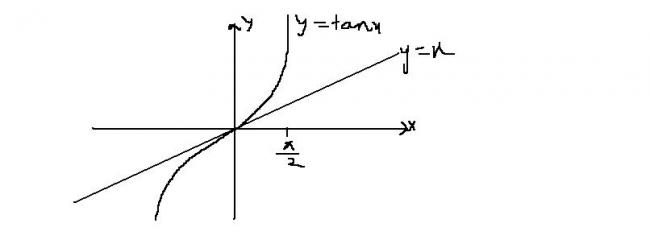

UP 0 DOWN 0
Post on FacebookPost anonymously?

11

Devil ·2009-11-20 23:55:42

derivative of tanx is sec²x, which is â‰¥1.

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Kaustab Sarkar ·2009-11-21 00:23:57

ok thanq everyone... i got it :)

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Kaustab Sarkar ·2009-11-21 00:26:30

one more

prove taht f(x)=(1+1x)^1/x is monotonically increasing in its domain

and draw its graph also :)

UP 0 DOWN 0
Post on FacebookPost anonymously?

Your Answer

Basic Integral Calculus Operators Symbols Matrix Cases

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω