1since it is "may be" so with out drawing exactly 4 tangents we can actually draw 3 tangents
Consider the curve \mid y\mid =\mid x 2 - 4\mid x\mid \mid
A) Area bounded by curve is 128/3 sq.units.
B) Area bounded by curve is 64/3 sq. units.
C) Number of tangents drawn from (8,0) may be 4.
D) Number of tangents drawn from (8,0) may be 3.
-
UP 0 DOWN 0 0 3
3 Answers
66In the first quadrant x≥0, y≥0, so the graph is simply y = |x2 - 4x| which is basically the parabola x2 - 4x with the part lying below the x axis reflected up.
In the second quadrant, x<0, y≥0, so the graph is y = |x2 + 4x|
In the third quadrant, x<0, y<0, so the graph is -y = |x2 + 4x| i.e. y=-|x2 + 4x|.
And in the fourth quadrant, x≥0, y<0, so the graph is -y = |x2 - 4x| i.e. y = -|x2 - 4x|.
Hence, the required graph is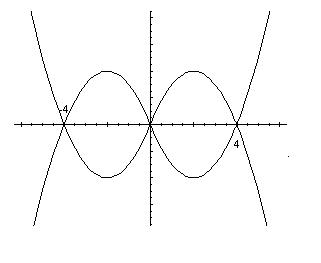
So the required area is 4 times
\int_0^4 (4x-x^2)\ \mathrm dx
i.e 4 323 = 1283
The number of tangents is obviously 4 which could be drawn from (8,0).
106I think aakash has made a mistake by giving ans as ACD
How can you have "maybe 3 tangents" when exactly 4 are possible?
1