
QUES 7: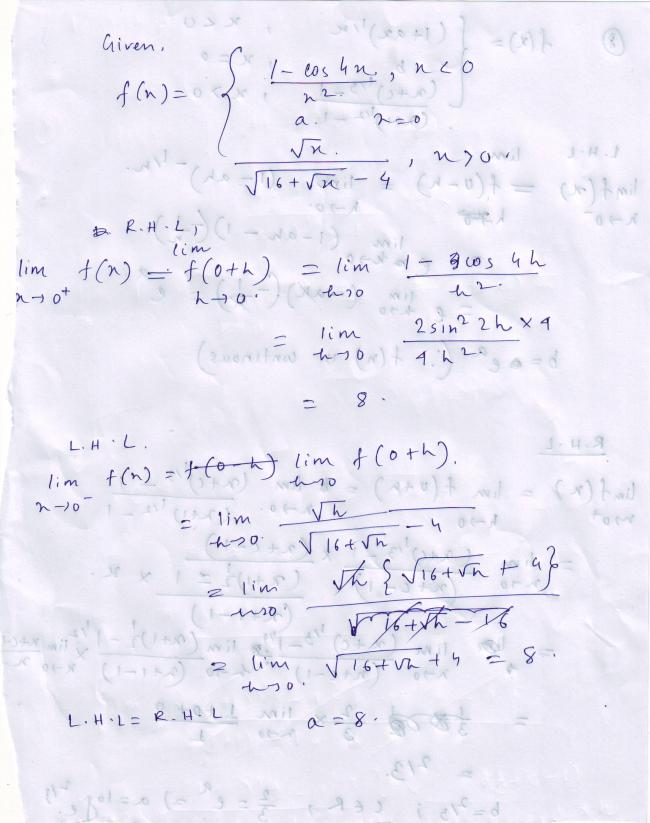

Q10)
Putting x = 0 , y =0 we get f(0) = 0
again putting y = -x we get f(x) + f(-x) = 0 → f(x) is odd function
f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}\frac{f(x+h)+f(-x)}{h}
=\lim_{h\rightarrow 0}\frac{f\left(\frac{h}{1+x^{2}+hx} \right)}{\left(\frac{h}{1+x^{2}+hx} \right)}.\frac{1}{1+x^{2}+hx} = \frac{2}{1+x^{2}}
so
f (x) =2tan-1x+c
f(0) = c hence c = 0
thus f(x) = 2tan-1x
so f(1/√3) = \frac{\pi }{3}
and f ' (1 ) = 1
Yup and that is why i always say that there should be seperate threads for seperate questions.
There will always be a couple of users who will just dump questions. We need to dump them [6]
I just hope we havent completed someone's homework.
When so many problems are dumped at one shot, my policy is to ask the OP for his attempt before answering.
11 . b >
lim ( 2h + 2 ) f ' ( h 2 + 2 h + 2 ) ( - 2h + 1 ) f ' ( - h 2 + h + 1 ) ............ after applying L - Hospital
= 2 f ' ( 2 )f ' ( 1 ) .............Putting h = 0
= 3
Q1)
Putting y = 0 and f(0) = 1 in given relation
f(x/2) = 12[f(x)+1]
so f(x) = 2.f(x/2) - 1
now f ' (x) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}\frac{1}{h}\left[ \frac{f(2x)+f(2h)}{2} -f(x)\right] = \lim_{h\rightarrow 0}\frac{1}{h}\left[\frac{(2f(x)-1)+(2f(h)-1)}{2} -f(x)\right]
\lim_{h\rightarrow 0}\frac{1}{h}[f(h)-1]=\lim_{h\rightarrow 0}\frac{f(h)-f(0)}{h}=f'(0)=-1
hence f ' (x) = - 1
f(x) = -x + c
putting x = 0 , f(0) = c = 1
so f(x) = 1 - x
f(2) = - 1
16) Writing series as-
cosx2n. cosx2n-1........cosx2 (n terms)
Using the relation-
CosA.Cos2A.Cos22A.....Cos2n-1A = Sin(2nA)2n.Sin(A)
Which makes the series bog dwn to-
Lim(n→∞) Sin2n(x/2n)2n.Sin(x/2n)
Then, use series expansion fr --- Sinx2n (n→∞).
The resultant answer comes = Sin(x)x
Q16)
let P = given limit
P = \lim_{n\rightarrow \infty }\left(\frac{2sin\frac{x}{2^{n}}cos\frac{x}{2^{n}}cos\frac{x}{2^{n-1}}......cos\frac{x}{2}}{2sin\frac{x}{2^{n}}} \right)
= \lim_{n\rightarrow \infty }\left(\frac{2sin\frac{x}{2^{n-1}}cos\frac{x}{2^{n-1}}cos\frac{x}{2^{n-2}}......cos\frac{x}{2}}{2.2sin\frac{x}{2^{n}}} \right)
= \lim_{n\rightarrow \infty }\left(\frac{sin\frac{x}{2^{n-2}}......cos\frac{x}{2^{2}}cos\frac{x}{2}}{2^{2}sin\frac{x}{2^{n}}} \right)
= \lim_{n\rightarrow \infty }\left(\frac{sinx}{2^{n}sin\frac{x}{2^{n}}} \right) (SIMILARLY)
= \lim_{n\rightarrow \infty }\left(\frac{sinx}{x} .\frac{1}{\left(\frac{sin\frac{x}{2^{n}}}{\frac{x}{2^{n}}} \right)}\right)
= \frac{sinx}{x}\lim_{n\rightarrow \infty }\frac{(x/2^{n})}{sin(x/2^{n})}
= \frac{sinx}{x}.1 = \frac{sinx}{}x
I think these questions are from the MATHIIT leaflet..:)
Q17)
let P = \lim_{x\rightarrow 0}\left(\frac{(1+\left\{x \right\})^{1/\left\{x \right\}}}{e} \right)^{1/\left\{x \right\}}
= \lim_{x\rightarrow 0}\left(\frac{(1+x-[x])^{1/x-[x]}}{e} \right)^{1/x-[x]}
LHL = \lim_{x\rightarrow 0}\left(\frac{(1-h-[0-h])^{1/0-h-[0-h]}}{e} \right)^{1/0-h-[0-h]}
= \lim_{x\rightarrow 0}\left(\frac{(1-h +1)^{1/\left( -h+1\right)}}{e} \right)^{1/(-h+1)} =\frac{2}{e}
and RHL = \lim_{x\rightarrow 0}\left(\frac{(1+h-[h])^{1/h-[h]}}{e} \right)^{1/h-[h]}
= \lim_{x\rightarrow 0}\left(\frac{(1+h)^{1/h}}{e} \right)^{1/h}
= \lim_{x\rightarrow 0}\left(\frac{e^{(1/h)ln(1+h)}}{e} \right)^{1/h}
= \lim_{x\rightarrow 0}e^{\left(\frac{ln(1+h)}{h}-1 \right)^{1/h}}
= \lim_{x\rightarrow 0}e^{\left(\frac{ln(1+h)}{h^{2}} \right)}
= e^{\lim_{x\rightarrow 0}{\left(\frac{\frac{ln(1+h)}{e^{h}}}{h^{2}} \right)}}
= e^{\lim_{x\rightarrow 0}}^{\frac{ln\left(1+\frac{1+h-e^{h}}{e^{h}} \right)}{(1+h-e^{h}/e^{h})}.\left(\frac{1+h-e^{h}}{e^{h}h^{2}} \right)}
= e^{\lim_{x\rightarrow 0}}^{\frac{ln\left(1+\frac{1+h-e^{h}}{e^{h}} \right)}{(1+h-e^{h}/e^{h})}.lim_{x\rightarrow 0}\left(\frac{1+h-e^{h}}{e^{h}h^{2}} \right)}
= eRQ (say)
here Q = lim_{h\rightarrow 0}\left(\frac{1+h-e^{h}}{e^{h}h^{2}} \right)
put h = 2t
Q = lim_{h\rightarrow 0}\left(\frac{1+2t-e^{2t}}{e^{2t}(2t)^{2}} \right)
= \frac{1}{4}lim_{h\rightarrow 0}\frac{-(e^{t}-1)^{2}+2-2e^{t}+2t}{e^{2t}.t^{2}}
= Q=\frac{1}{4}\left\{-(1)^{2} +2Q\right\}\Rightarrow 2Q=-1 \Rightarrow Q=\frac{-1}{2} & R = 1
hence RHL = e-1/2
since LHL ≠RHL
limit doesn't exist
9 > f ( x ) = ( x ) ( e )- [ 2x ] , for , x > 0
= ( x ) ( e ) 0 = x , for , x < 0
= 0 , for , x = 0
Clearly , L . H . L = R . H . L = Functional value at x = 0
So , f ( x ) is continuos .
As f ( x ) is continuos , hence we can directly differentiate and hence test differentiabilty .
f ' ( x ) = ( 2x ) ( e ) [ - 2x ] , for x > 0
= 1 . for x < 0
= 0 , for x = 0
Clearly , f ' ( x ) is discontinuos at x = 0 .
Hence . f ( x ) is not differentiable for x = 0 .
10 > f ( x ) = a tan -1 x ,
Now , from the given limit , a = 2
Hence , f ( x ) = 2 tan - 1 x
So , f ( 1 / √3 ) = 2 Î / 6 = Î / 3
And f ' ( 1 ) = 2 / [ 1 + 1 ] = 1
5 > Same thing as in 1 , f ( x ) = a x + b
Here , a = 1 , as f ' ( 0 ) = 1 .
So , f ( x ) = x + b , which clearly is continuos for all x .
1 > The relation given only satisfies , f ( x ) = a x + b , where a and b are any real numbers .
I can prove it if you like ,
Given , f ' ( 0 ) = - 1
So , a = - 1
And , f ( 0 ) = 1
So , b = 1
Hence , f ( 2 ) = - 1
Q11(a)
\lim_{x\rightarrow 2}\left(\frac{xf(2)-2f(x)}{x-2} \right)
using L hospital rule
\lim_{x\rightarrow 2}\left(\frac{\left\{f(2) \right\}-2f'(x)}{1} \right)
now substitute x = 2
so limit reduces to 4 - 2 x 11 = 2
Q6) Limit = \lim_{x\rightarrow 0}\frac{a(e^{x}+xe^{x})-b.\frac{1}{1+x}+c(e^{-x}-xe^{-x})}{2xsinx+x^{2}cosx} [ using L H rule ]
= a - b + c0 = \infty unless a - b + c =0
but given limit is 2 so inderterminate form 0/0 shuld continue
so a - b + c = 0 .............................(1)
then limit , [ using LH rule ]
= \lim_{x\rightarrow 0} \frac{\left\{a(1+x)e^{x}+ae^{x}+\frac{b}{(1+x)^{2}}+c(-1)e^{-x} +c(1-x)e^{-x}.(-1)\right\}}{2sinx+2xcoxsx+2xcosx-x^{2}sinx}
= \lim_{x\rightarrow 0} \frac{\left\{a(2+x)e^{x}+\frac{b}{(1+x)^{2}} -c(2-x)e^{-x}\right\}}{2sinx+4xcoxsx-x^{2}sinx}
= \frac{2a+b-2c}0{} = \infty unless 2a + b - 2c = 0
but limit = 2
so, 2a + b - 2c = 0 .............................(2)
then limit = \lim_{x\rightarrow 0} \frac{\left\{a(2+x)e^{x}+ae^{x}-\frac{2b}{(1+x)^{3}}+c(2-x)e^{-x}+ce^{-x} \right\}}{6cosx-4xsinx-2xsinx-x^{2}cosx}
= 2a + a - 2b + 2c + c6 = 2 (given )
hence 3a - 2b + 3c = 12 .............................(3)
solving equation (1) , (2) and (3) we get
a = 3 , b = 12 , c = 9 .
Q3 (b)
\lim_{x\rightarrow \infty }\left(\frac{x^{2}+1}{x+1}-ax-b \right) = 0
\lim_{x\rightarrow \infty }\left(\frac{x^{2}+1-(ax+b)(x+1)}{x+1} \right) = 0
\lim_{x\rightarrow \infty }\left(\frac{x^{2}(1-a)-(a+b)x-b+1}{x+1} \right) = 0
1-a = 0 , a+b = 0
so a = 1 and b = -1