3let n be 1
and therefore f'(x)=k(x2-1)k-12x
has three real roots and we need 7 more roots to get the given condn and so the other roots shud be imaginary which can be possible if k=9
Let f (x) = (x2 -1)k where k belongs to N. The number of distinct real roots of equation f n (x) = 0 are 'm' (where f n (x) denotes the nth derivative of f (x)). If 'm' equals to 10 for exactly one value of 'n' , then k equals to
1. 8
2. 9
3. 10
4. 11
-
UP 0 DOWN 0 0 31
31 Answers
3
3@subash the graph for the function (x^2-1)^9
shud be like this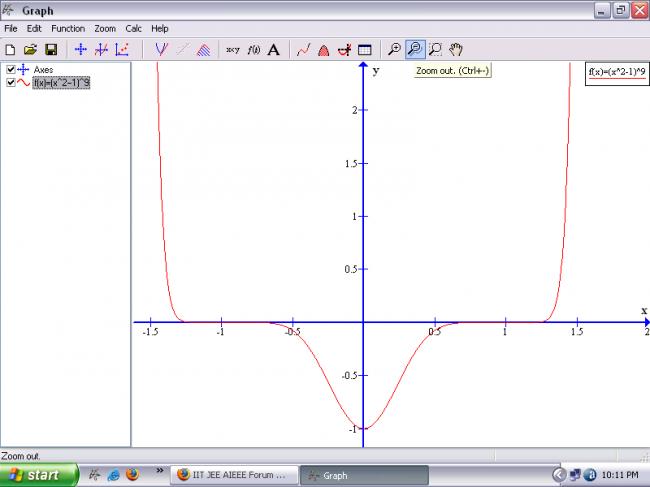
so the given function cant have more than two real roots therefore the qn is rong
33[3]
wo nahi.. ek stupid sa q post kiye the.. post karte sath samjh me a gaya.. so mita diye... but agar koi padh lliya hoga isliye... upar wala post kiye...
3i will do such assumptions in exams da.unfortunately it will get me +ive marks for a gr8er xtent
3dont know whether it is a right approach
we will wait for mathematicians of targetiit
3dont call him stupid da
becos he was miles higher than me
so if u call him stupid then
i am (very)milesstupid
1ya sorry sanky......................i think its integration.........stupid subash tryin 2 confuse me hehehehehe
1u sure tht ques is rite??? coz f(x) can be diff only thrice......so fn is meaningless........n can be 1,2,3.......rite???
AM I WRONG??
3my dear akand .clearly the eqn is quadratic.its derivative cant have more than two roots but in the option it is given dat the roots are higher than two.