21@ Rahul ur answers are correct
Try the 2nd one .
This may reduce ur hardwork mannyy times http://sanjosemathcircle.org/handouts/2007-2008/20071114.pdf
1) In triangle ABC, E is on AC so that CE = 3AE and F is on AB so that BF = 3AF. If BE and CF intersect at O and line AO intersects BC at D, compute OBOE and ODOA.
2) In triangle ABC, points D and E are on sides BC and CA respectively, and points F and G are on side AB. BE intersects CF at point O1 and BE intersects DG at point O2. If FG = 1, AE = AF = DB = DC = 2, and BG = CE = 3, compute O1O2BE.
Source: www.wikipedia.org
-
UP 0 DOWN 0 0 2
2 Answers
36I hope this helps
I m just doing it using Thales' theorem... the only one i know for these sort of sums...
1>
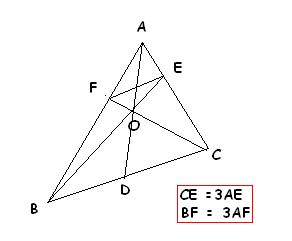
we draw the figure as per the question. Now,
AF/BF = AE/CE = 1/3
so, EF || BC [by Thales' theorem]
=> ∆EOF ~ ∆BOC
=> OB/OE = BC/EF
Now, clearly, ∆AEF ~ ∆ACB [since EF || BC]
so, AB/AF = BC/EF
now, BF/AF = 3 => BF/AF + 1 = 3 + 1 => (BF + AF)/AF = 4 => AB/AF = 4
=> BC/EF = 4
Thus, OB/OE = 4 ...
Next comes,
OD/OA [the biggest tension of this problem]
Again, do this construction inside the triangle and name the points...
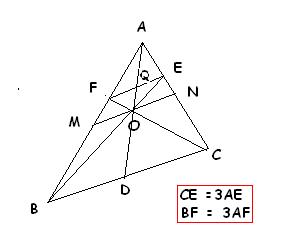
clearly, ∆OEQ ~ ∆OBD [by AAA]
so, OD/OQ = OB/OE = 4
=>(OD + OQ)/OQ = 5
=> DQ/OQ = 5 ---- (i)
and, AQ/QD = 1/3 ---- (ii)
(i) x (ii)
AQ/OQ = 5/3
=> (AQ + OQ)/OQ = (5 + 3)/3
=> AO/OQ = 8/3 ---- (iii)
and, OQ/OD = 1/4 --- (iv)
on, (iii) x (iv) we have,
OA/OD = 2/3 Ans..
Hence, OB/OE = 4 and OD/OA = 3/2
sorry.. if there r lill errors... and i know it must me wrong... coz i've solved it...
21