36wowo.. no one... well that's good...!!
hint... the question is right
the radii of two concentric circles are 13cm and 8cm . AB is diameter of bigger circle. BD is tangent to the smaller circle touching it at D . find the length of AD?
-
UP 0 DOWN 0 0 12
12 Answers
1See i am in a hurry therefore posting a solution but i dont think its tenth level solution. But its an easy solution
Let O be the center of the circles.Join AD
Now in triangle ADB Od is the median .
By using Stewarts theorem ( if u dont know it please see http://en.wikipedia.org/wiki/Stewart's_theorem as it is very helpful in solving olympiad questions if u r interested in them)
we get
13AD2 + 13 BD2 = 26 ( 64 + 132)
Solving it we get
AD = 19 cm
:)
21
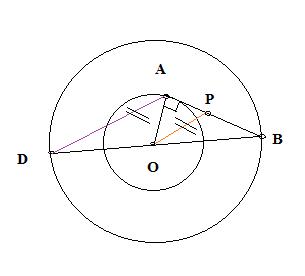
From Right angled Triangle AOB ,AB = √105.. P bisects AB so AP = 1/2*√105. Again from Triangle AOP OP = 9.5 so AD = 2*OP = 19 ;)
1I used the pythagorean theorem to find out AD, then used the law of cosines to figure out angle AOB and angle ABD. I used the law of cosines again to find out AB since we knew two sides and an angle.
1I used the pythagorean theorem to find out AD, then used the law of cosines to figure out angle AOB and angle ABD. I used the law of cosines again to find out AB since we knew two sides and an angle.
1I used the pythagorean theorem to find out AD, then used the law of cosines to figure out angle AOB and angle ABD. I used the law of cosines again to find out AB since we knew two sides and an angle.
1I used the pythagorean theorem to find out AD, then used the law of cosines to figure out angle AOB and angle ABD. I used the law of cosines again to find out AB since we knew two sides and an angle.
1I used the pythagorean theorem to find out AD, then used the law of cosines to figure out angle AOB and angle ABD. I used the law of cosines again to find out AB since we knew two sides and an angle.
