The section consists of a few questions. Just work them out... I too wanna check myself..
1. If, (a + 2b)2 + (b - 2c)2 + (c - 2a)2 = 0 find (a + b - c)2 where, a,b and c belongs to R.
2. We have three triangles in the figure below.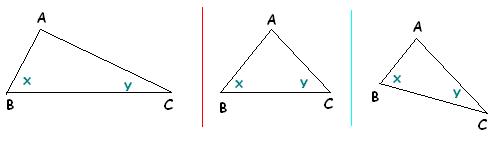
In the first figure we have, x > y in the second we have x = y and in third we have x = 2y
which of these are true and why/why not?
i. AC > AB ii. AB = AC iii. AC = 2AB
3. If (tan A + cot A) + (sec A + cosec A) = m and, (sec A - tan A) = p and (cosec A - cot A) = q
then prove that, p, 2/m and q are in H.P
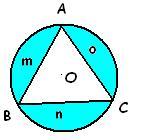
4. In the figure below we've a circle C (O,r) where r = 4 cm. An equilateral triangle ABC is drawn inside it. The three shaded regions are marked as m,n and o respectively.
Then, (m + n + o) / (AB + BC + AC) = .................. centimetres
5. Which of the following values of a,b,c and d will make the quadrilateral ABCD a beautiful trapezium.
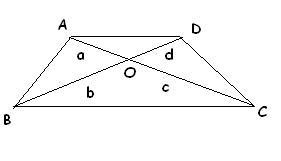
i > a = 5 , b = 12 , c = 10 , d = 6
ii > a = 2 , b = 4 , c = 6 and d = 8
iii > a = 2 , b = 5 , c = 18 and d = 13
iv > a = 3 , b = 8 , c = 6 and d = 4
6. If a2 + b2 = m where, a and b are integers. Let there be another integer q which comes out to be the quotient on dividing m by 2 then which of the following values can m can't take
i> m = 2q + 1
ii> m = 2q + 3
iii> m = 2q
iv> m = 2q + 2
v> m = 2q + 11
vi> m = 2q + 1050
I can't take the guarantee that all the questions are correct or not. But will post the solution. I swear!!!! :P
36lemme work out the first one..
1>
given, a,b,c are real numbers....
and, (a + 2b)2 + (b - 2c)2 + (c - 2a)2 = 0
so, clearly, (a + 2b) = 0 , (b - 2c) = 0 and (c - 2a) = 0
Now,
(a + b - c)2 = a2 + b2 + c2 + 2ab - 2bc - 2ac = a (a + 2b) + b (b - 2c) + c(c - 2a)
= a(0) + b(0) + c(0) = 0
36wow.. no one is giving it a try.... they r dead easy and interesting...!!
10th level probos
36Solution to Q3
(tan A + cot A) + (sec A + cosec A) = m
=> (sec A + tan A) + (cosec A + cot A) = m
=> [(sec A + tan A)(sec A - tan A)]/(sec A - tan A) + [(cosec A + cot A)(cosec A - cot A)]/(cosec A - cot A) = m
=> 1/(sec A - tan A) + 1/(cosec A - cot A) = m
=> 1/p + 1/q = m
=> m = (p + q)/pq
=> 2/m = 2pq/(p + q)
so: p, 2/m and q are in H.P done... :D