Try if you can:P

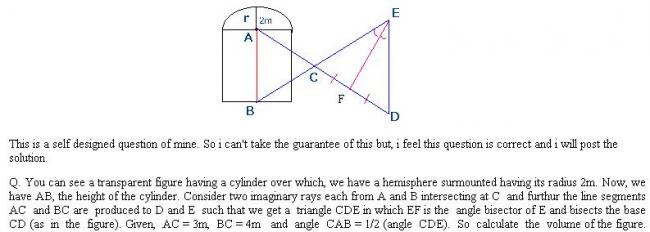
well i knew that

First of all in ∆CDE we have,

∆CFE = ∆DFE (by SSA) or, u can use the angle bisector theorem that CE/DE = CF/DF and so...

So, we have Triangle CDE is isocelous
-> LCDE = LDCE
-> LACB = LCDE

As per the question,
LCAB = 1/2 LACB
So, in triangle ACB we have,
c² = a(a + b) or, AB² = BC(BC + AC)
or, AB² = 4(4 + 3)
-> AB² = 28
-> AB = 2√7 m

Thus, Area of the figure = Area of the hemisphere + Area of the cylinder
= 2/3 x pi x 8 + pi x 4 x 2√7 = 16pi/3 + 8√7 pi = 3.14(5.33 + 21.17)
= 83.21 m³ Approx.... Wasn't that a good question!!