\hspace{-16}$In a $\bf{â–³ABC}$ If $\bf{P}$ be a point which is Inside the $\bf{â–³ABC}$ such that\\\\ Area of $\bf{â–³APB=}$ Area of $\bf{â–³BPC=}$ Area of $\bf{â–³CPA}$.\\\\ Then prove that the point $\bf{P}$ is the centroid of $\bf{â–³ABC}$
plz provide detailed solution.
Thanks
-
UP 0 DOWN 0 0 1
1 Answers
2305
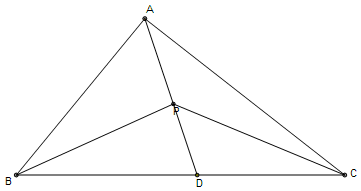
Let P be the centroid of the triangle.
Let BD = CD,
Area of :\bigtriangleup ABD = \bigtriangleup ACD
(since the base length and height are the same)
Similarly,
Area of :\bigtriangleup PBD = \bigtriangleup PCD
Therefore,
Area of :\bigtriangleup ABD-\bigtriangleup PBD = \bigtriangleup ACD-\bigtriangleup PCD
\bigtriangleup APB = \bigtriangleup APC
Similarly,
\bigtriangleup APB = \bigtriangleup BPC
\bigtriangleup APB = \bigtriangleup BPC = \bigtriangleup APC
The only thing left to prove is that only one point in a triangle satisfies the given condition.
This is easy to see since if we move the point P from the centroid in a particular direction the area of at least one of the 3 triangles will increase and the area of at least one will decrease.
man111 singh Thanking You. very Nice explanation man.Upvote·0· Reply ·2013-02-28 06:39:20