11ISKA ANSWER KYA HAI ?????
COULD SOMEONE CONFIRM!!!!
from an arbitrary point p on the circle x2+y2=9,tangents are drawn the circle x2+y2=1 andwhich meet the circle x2+y2=9 at A and B .locus of points of intersection of tangents from A and B. is
(subjective type)
-
UP 0 DOWN 0 0 20
20 Answers
1don't give questions which have no answer
or u don't have any solution 4 it
or tell the answer of this one [16]
11x,y be the Point p
From this x,y the tangents are drawn
y = mx + a√(1+m2)
Let
y2+ m2x2 - 2ymx = a2 +a2m2
m2(x2-a2)-2yxm + y2 - a2 = 0
r & q be the roots of the above
r or q ={ 2yx ± √4y2x2 - 4(x2 - a2)(y2-a2)}/2(x2-a2)
a = 1
{ 2yx ± √4y2x2 - 4(x2 - 1)(y2-1)}/2(x2-1)
{2yx ± √ 4(y2x2 - x2y2 +x2 +y2 - 1)}/2(x2-1)
r or q = 2yx ± 2√8/(2(x2 -1)
r or q = yx ± 2√2/(x2-1)
Now consider x = x1
y = y1
r and q are slopes.
Eq of the line is
y - y1= y1x1 ± 2√2/(x21-1)[(x - x1)]
Now this line concindes with x2 + y 2 = 9
Now i am getting tired will do it later
62I think there is some issue with these solutions..
as much as i understood the question, both these solutions are wrong!
1find the trick involved[1],otherwise u"ll waste a lot of time solving it conventionally
11@deep iss mein kya samajh nahin aaya
pehle equation of chord likh di fir uska distance choote circle se 1 hai
using these 2 conditions i got the answer
1
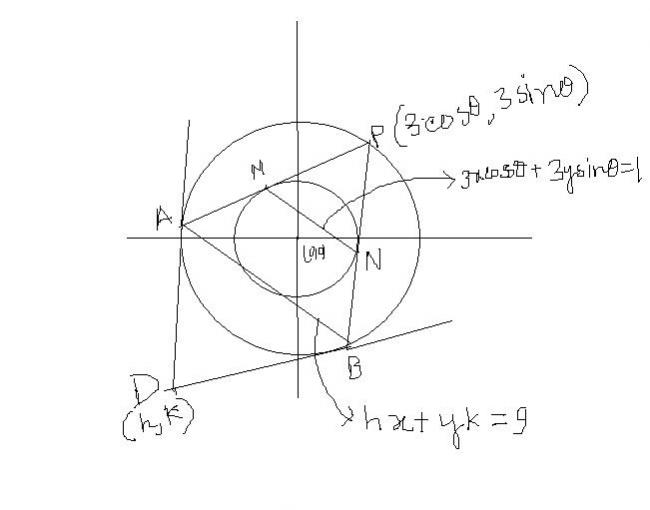
chord of contact of D on big circle is parallel to chord of contact from P on small circle.
so, we have, -h/k = - cotθ => h/k=cotθ ---------#1.
11I WAS WRONG IN SAYING THAT
SORRY 4 THE MISCONCEPT
BUT NOW I THINK THIS FIGURE COULD TELL THE WHOE STORY
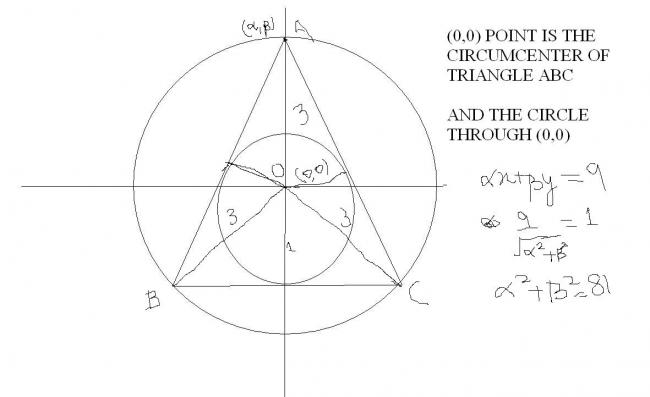
13maniboy can u plz prove it to my how is it an equilateral triangle and how did u get thAT AS UR LOCUS
1@wats in name? :P
areey yarr kya kar rahe ho i said abt the trick involved in solving!!!
