Circle and a parabola

one thing, the chord of contact will be symmetrical wrt x-axis..
(since both circle n parabola are symmetrical to x-axis..)

let radius be 'r'.

take the two extremities of chord of contact as A(rcosθ1, rsinθ1)
and B(rcosθ2, rsinθ2).

but since the line is symm with x-axis, θ2=θ1.
so the two points become A(rcosθ1, rsinθ1) and B(rcosθ1, -rsinθ1).

given that the ch of contact subtends a r8 angle at vertex i.e. (0,0)

so m1.m2 =-1.
from here we get sin²Î¸1/cos²Î¸1 = 1
=> tanθ= +- 1. => θ=Π/4, -Π/4.

These points also lie on the parabola.

so (rcos pi/4 , rsin pi/4) must satisfy parabola eqn.

then r= 4√2.

you should note that the centre of the circle is not origin but is at (-2,0)

Co-ordinates of the end points of the chord can be found by what you suggested.

The radius will simply then be the distance between either of these points to the centre of the circle.

say the cordinates are (h,k) and (h,-k)

since product of slopes =-1
implies k=±h

so the points will be (h,h) and (h,-h)

since it lies on parabola
implies h=4

hence radius =√6²+4²

mughe yeh samaj me nahi araha ki aap logon ne kaise centre of the circle ko (-2, 0) liya ?

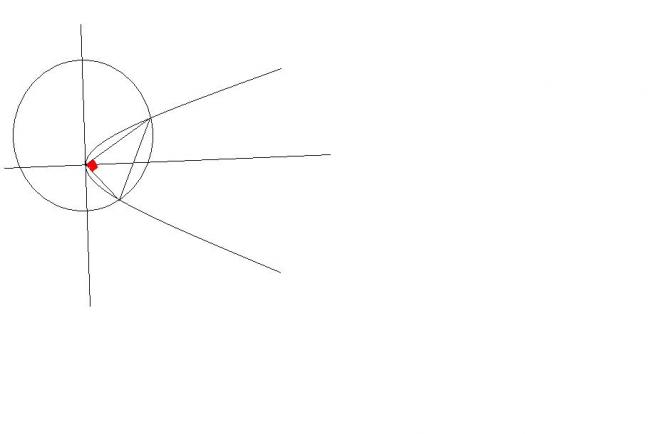
the one shown in the diagram is also possbile no?

mera doubt clear karo koi ? sorry if it's dumb.

here's the figure.
this is also possible no?

Hey I think the question was edited after sonls.... so the solns are not looking appropriate