Altitude of the triangle of maximum area that can be inscribed in the curve [modulus of{z-2-2i}]=4 or (x-2)2 + (y-2)2 =4 is what?
62This is a circle of radius 2 units
Now you have to inscribe a triangle in it..
So you have to solve this geometrically..
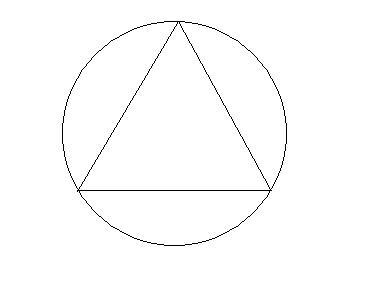
1Is there any other method we can use apart from the one given below?:
Treat the circle as x2 + y2=22 .Take the point (2,0) as z1=2. Then, we use z2/z1=(r2/r1)e(iθ), where z2 is the complex number corresponding to a point obtained by rotating z1 vector by 120°(anticlockwise),r1=r2=2,θ=120° and e(iθ)=(cosθ + isinθ).We then find length of the line segment joining z1 and z2.
Then we proceed as per geometry.
Any other shorter method please?
62Nikhil, You have missed the whole point
See the thing here is that the triangle here has been inscribed in the circle..
height of the circle is maximum if it is a isosceles triangle.
There is very little calculation required..
hence what we get here is that the triangle for any given base will have other two sides equal...
Hence, the triangle will be equilateral
see the image
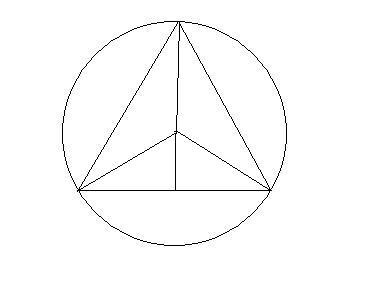
Here we can get the height as R+ R Sin 30 = R(1+/2) = 3