11
Let T1, T2 be two tangents drawn from (-2,0) oneo the circle C:x2+y2=1. Determine thecircles touching C and having T1, T2 as their pair of tangents. Further, find the equations of all possible common tangents to these circles taken 2 at a time.
-
UP 0 DOWN 0 0 3
3 Answers
11AREY, SOMEONE GIVE THE ANALYTICAL TREATEMENT TO THIS QUESTION!!!! I'VE DONE ALL I COULD DO
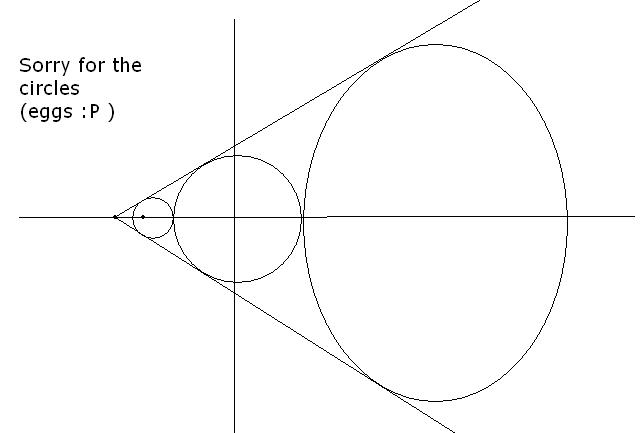
1If Ap and AQ are the two tangents and angleOAP=theta
sion(theta)=1/2 theta=30
equations of AP and AQ are y=1(x+2)/√3 and y=-1(x+2)/√3
if C(h,0) be the center of a circle touching the given circle and touching AP and AQ then CL/OP=AC/AO
(-1)-h/1 =h+2/2
h=-4/3
the equation of the circle is (x+4/3)2+y2=(1/3)2
if D(h1,0) is the center of the other circle touching the given cirlce and the lines AP and AQ then AO/AD=OP/DM
2/2+h1=1/h1-1
therefore h1=4
the equatuion of the second circle is (x-4)2+y2=32
the transverse common tangents divide the line of centres in the ratio of the radii 1/3 to 3
the point of division is N(-4/5 ,0)
let the tangent from N to the second circle be y=m(x+4/5) the condition of tangency to the second circle is given by |24m/5 /√1+m2| =3
this gives m= 5/√39or -5/√39
and the two tangents are y=5(x+4/5)/√39 and -5(x+4/5)/√39