Let 2x^2+y^2-3xy=0 be the eqn of a pair of tangents from the origin to a circle of radius 3 ,with centre in first quadrant,find the distance from O to the pt of contacts
-
UP 0 DOWN 0 0 5
5 Answers
62Vivek, try applying geometry, specially to such sums of circles
invariably it will help a lot
This one is another such case
just draw the straigh lines and the circle the rest will follow :)
12x2+y2-3xy=0
i.e (y-x)(y-2x)=0
lines are y=x and y=2x
let C(a,b) be the center of the circle whose tangents are two lines y=x and y=2x
clearly b>a and b<2a
radius=3=length of perpendicular from C on the two tangents
=b-a/√2 = 2a-b/√5
from above, a=3(√5+√2) and b = 3(√5+2√2)
OA2=OC2- radius2
=(a2+b2-9
=9(7+2√10)+9(5+8+4√10)-9
=171+54√10=90+81+2√90x81=(√90+√81)2
therefroe OA=9+√90=9+3√10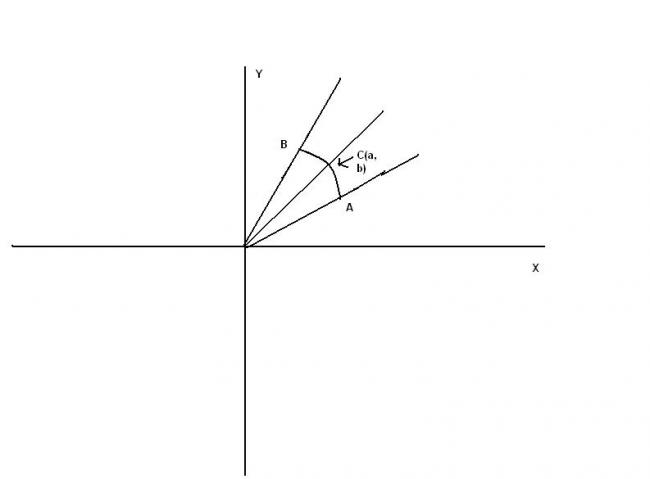
1@genius,ur answer is correct,i was also thinking abt ths same method when u posted it,coincidence!!
@Nishant sir,i would like to know abt the geometrical method too,if its different and shorter than the above one
62no vivek
this only
see that once you have drawn the graph there was no coordinate involved.. that is what i was saying