1
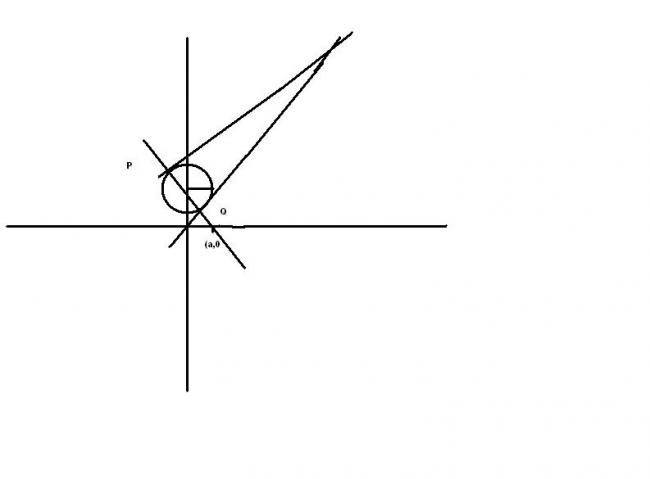
this will the diagram
A circle with radius a and centre on y - axis slides along it and a variable line through (a,0) cuts the circle at points P and Q. What is the region in which the pt of intersection of tangents to the circle at points P and Q lies ?
-
UP 0 DOWN 0 0 16
16 Answers
11hey guys,
let the circle be x2+(y-k)2=a2
let (p,q) be a point on the required locus
from data xp+(y-k)(y-q)=a2(chord of contact from (p,q))
this passes through (a,0)
thus ap+k(k-q)=a2
ie k2-qk=ap-a2=0
k is real hence discriminant>0
hence u get q2-4a(p-a)>0
hence the region is given by
Y2-4a(X-a)>0
it lies outide the obtained parabola
NOTE: LET ME KNOW IF I AM CORRRECT OR NOT(PLEASE)
1what does it mean by what is region in which the point of intersection lies??
1i thnk it means like the line through a,0 can be a tangent on either side... they are the limitinng cases...
oh//i cant express... trying to draw...
62I think we cando better than that sky....
because the location of the circle on the z axis is unknown..
1jaise jaise circle dur jaega dikkat hogi..[12]
jab origiin pe aaega or fir neeche jaega [12]
1base AB(=k units) of a triangle ABC is fixed ,vertex C moves in such a way that
sinA=θsinB (|θ|<1) ,
then locus of C is a circle whose center lies on base AB ,find the radius of this circle?