Is the answer b.\frac{\4 }{\Pi } ???????
Consider a parabola y=\frac{x^{2}}{4} and the point F (0, 1). Let A1(x1, y1), A2(x2, y2), A3(x3, y3),........, An(xn, yn) are 'n' points on the parabola such
xk > 0 and <OFA_{k}=\frac{k\Pi }{2n} (k=1,2,3,....,n). Then the
value of \lim_{n\rightarrow \infty }\frac{1}{n}\sum_{k=1}^{n}{FA_{k}}, is = ?
(A) \frac{2}{\Pi } (B) \frac{4}{\Pi } (C) \frac{\Pi }{\2 } (D) \frac{\Pi }{\4 }
-
UP 0 DOWN 0 0 4

4 Answers
let Ak=(2t,t2)
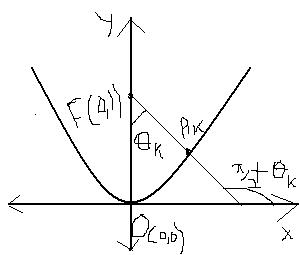
Slope of FAk = t2-12t-0 = tan(Π/2+θk)
tan θk = 2t/1-t2 = tan(2φ) (say)
so φ = θk2 = kΠ4n where tanφ = t
Also FAk = √(t2-1)2+(2t)2 = t2 + 1 = 1+tan2φ = sec2(kÎ /4n)
\lim_{n\rightarrow \infty }\frac{1}{n}\sum_{k=1}^{n}{FA_{k}} = \lim_{n\rightarrow \infty }\frac{1}{n}\sum_{k=1}^{n}{\sec ^{2}\left(\frac{\Pi }{4}(\frac{k}{n}) \right)} =
\int_{0}^{1}{\sec ^{2}\left(\frac{\Pi x}{4} \right)}dx. = \frac{4}{\Pi}\left[tan (\frac{\Pi x}{4}) \right]_{0}^{1}= \frac{4}{\Pi }