FInd the length

VITEEE 2015 Guidance › Co-ordinate Geometry questions › FInd the length

Given a circle with center at ' A ' which touches the X - Axis at ' B ' with radius 1 unit. ' C ' is the origin from which a tangent at ' E ' is drawn to me line through ' AB ' at ' D ' such that angle ' CBD ' = 90Â°.

The perimeter of the triangle ' CBD ' is 8 units. Then find the length of ' AD '.

#Mathematics #Co-ordinate Geometry

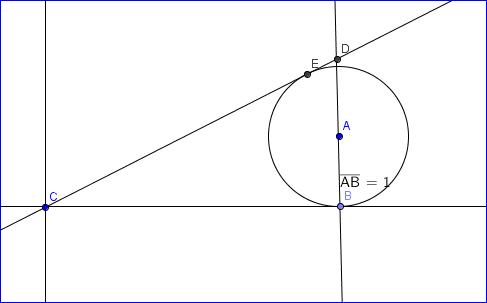
UP 0 DOWN 0 0 5
Post on FacebookPost anonymously?

5 Answers

1

rishabh ·2012-01-06 09:09:08

using the fact that tangents frm same point have same length we can say that CB = CE.
now,

perimeter of CBD = CB+CE+ED+AD+1
=> 8 = 2CB + ED+AD+1 ....(1)

since AED is right angle triangle so using pythagoras theorum,
1 + ED² = AD² ....(2)

since CBD is right angled triangle so using pythagoras theorum,

CB² + (1+AD)² = (CB+ED)² ....(3)

you have 3 eqns. 3 unknowns which can be easily solved.

UP 0 DOWN 0
Post on FacebookPost anonymously?

71

Vivek @ Born this Way ·2012-01-07 05:50:59

Provide the answer please.

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

gty ·2012-01-08 08:11:26

ya i 2oo m nt getting the ryt ans................

UP 0 DOWN 0
Post on FacebookPost anonymously?

36

rahul ·2012-01-09 04:16:53

But I have some result nd hope its correct....
I guess its 5/3 units
Will post the sol later... if its correct

UP 0 DOWN 0
Post on FacebookPost anonymously?

71

Vivek @ Born this Way ·2012-01-09 05:43:47

Yes , 5/3 is correct.

@Rahulm, Do you have any other method than this to calculate easily.

UP 0 DOWN 0
Post on FacebookPost anonymously?

Your Answer

Basic Integral Calculus Operators Symbols Matrix Cases

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω