24this much is clear......what next???????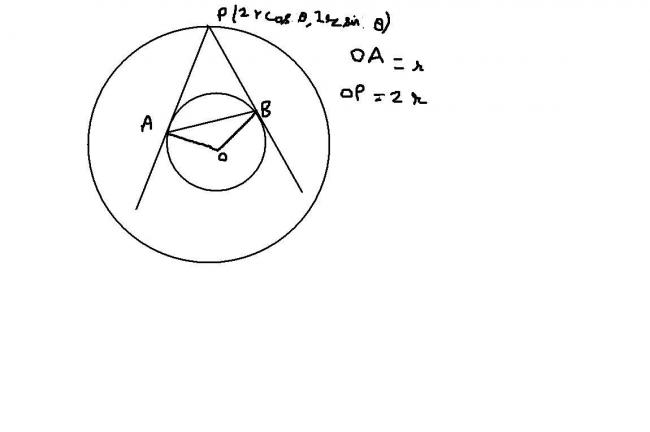
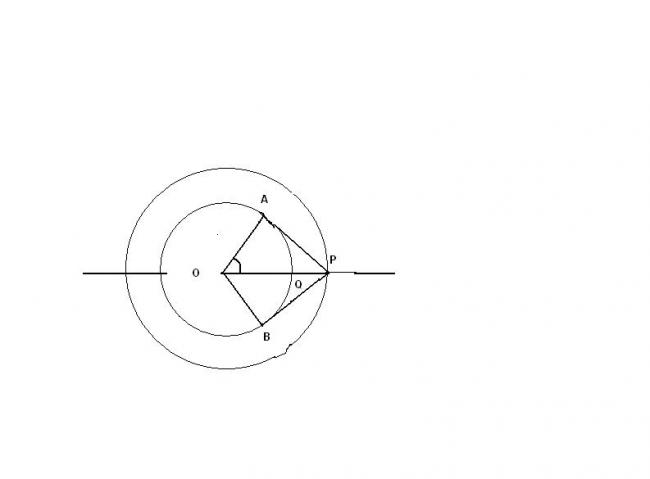
C1 andC2 aretwo concentric circles the radius of C2 being twice of C1 from a point P on C2, tangents PA andPB are drawn to C1. Prove that the centroid of the triangle PAB lies on C1
-
UP 0 DOWN 0 0 9
9 Answers
24i think P point isnt fixed so θ should vary..............[12]
i maybe wrong
1without loss of generality,
center i am taking as (0,0)
let P (x1,y1) be a point on the big circle. so, x12+y12=4r2
chord of contact on smaller circle : x.x1+y.y1=r2
omy god! power cut.. ! shit shit.
24oh thats a typing mistake.......i was writing 2r and then wrote 2θ......sorry
1let OP be x axis therefore P is (2r,0) and the equation of inner circle is x2+y2=r2
in triangle OAP, OA/OP=cos\Theta =r/2r=1/2
\Theta=60 , coordiantes of A are (rcos\Theta,rsin\Theta)=(r/2,r√3/2)
by symmetry co-ordinates of B are(r/2, -r√3/2)
G=[(2r+r/2+r/2)/3 , (0+r√3/2-r√3/2)/3]
=(r,0)
and this clearly lies on the inner circle
62I think it wud be slightly better if you could refine the proof!