Please suggest a shortcut , do we have no other way than writing the normal and finding it's intersection point?
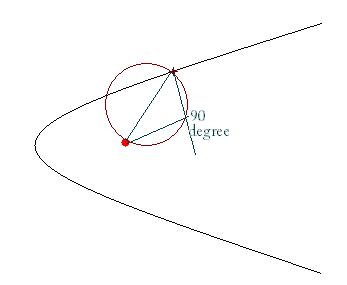
If the normal at the point P(at2 , 2at) to the parabola y2=4ax cuts the circle drawn with PS as diameter at Q ( S- focus ) P.T. PQ = a√( 1+t2)
-
UP 0 DOWN 0 0 11

11 Answers
you can solve it by geometry alone
take the angle between normal and diameter PS
Also the radius of the circle is simple to find...
I hope this is hint enuf?
I got the radius a(1+t2)/2 , then the angle between the normal and the radius is tanθ = t . then , the side opposite θ is tx and adjacent is x . So we ,get a√(1+t2) / 2 . thus the length is a√(1+t2)
Thank you!!!!!!!! Nishant . But just check if I've made any mistakes .You're an awesome teacher.
Thanks buddy :)
hey yeah there is a slight mistake.. u need to take diameter .. not radius :)
the right angled traingle has hypotenuse as D :)
hey there is another brilliant way to do this..
find the distance between the line through the focus and parallel to the tangent at P(at2 , 2at)
does this make sense?
or take radius and then , find half of the chord , we know θ and hypotenuse . perpendicular from center to chord bisects it.then we can double it. SAME , isn't it?
Thanks buddy :)