71Reviving this one.
1. A ball moving around the circular path x2+y2-2x-4y-20 = 0 in anticlockwise direction, leaves it tangentially at the point P (-2,-2), after which it rebounds from a a straight wall,and passes through the center of the circle.
Find the eqn. of the straight wall and the line of rebounding of the ball. The perpendicular distance of point P from the wall is 2.5 .
-
UP 0 DOWN 0 0 2
2 Answers
1
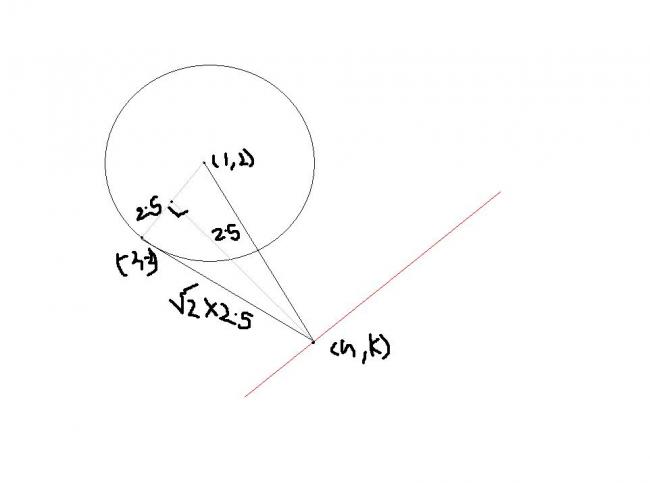
the tangent equation is
2x+3y=16
the point (h,k) lies at a distance of (√2*2.5) from the point (-2,-2) ,u can find it using parametric method
i.e
h+2=2.5*√2 3√13
k+2=-2.5*√2 2√13
now u can find the equation of rebonding wall by the point slope formula