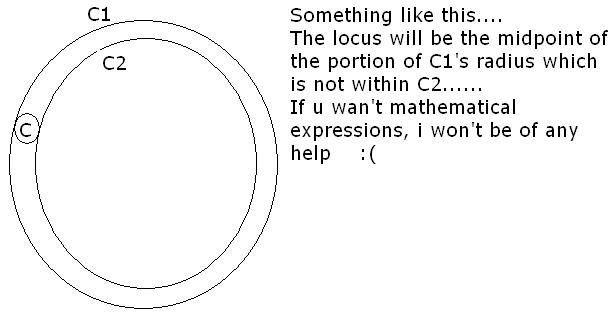
Let C1 and C2 be two cirlces with C2 lying inside C1. A circle C lying inside C1touces C1 internally and C2 externally. Identify the locus of the center of C
-
UP 0 DOWN 0 0 12

12 Answers
aaragon dont u think u have drawn a biased figure..........concentri isn't given
oopsie.....ya eureka....thanx for pointing out my mistake [4]
from, RQ+RP=r1+r2 , it looks like locus could be ellipse..............[12][12]
Bhaiya, if C2 were not fixed,,,,won't we get a region more than a locus??
sir aaj cam nahin hai
but the concept is
Let the radius of C1 be r1 and circle C2 be r2 and let the center of C1 be at (0,0) and C2 at (h,k)
equation of C1=> x2+y2=r12
equation of C2=> (x-a)2+(y-b)2=r22
let the center of C be (h,k)and be of radius r
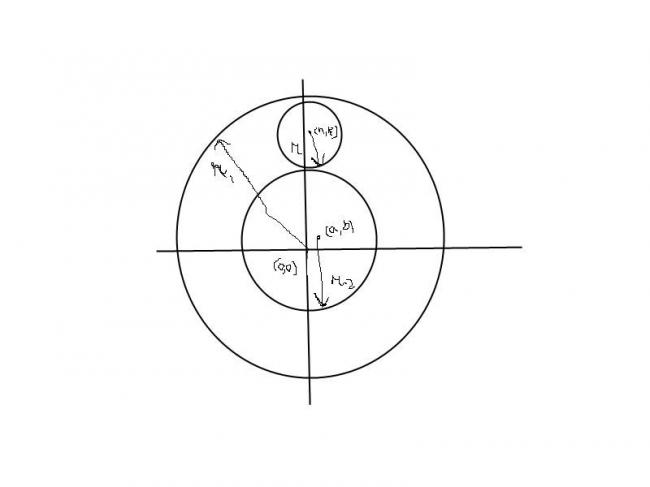
so
√(h-a)2+(y-b)2=r+r2 =A
√(h2+k2)=r1-r =B
So
we can see that A+b = constant
or
PS+PS`=constant
which is the locus of the ellipse at focii (a,b) and (0,0)

If C1 and C2 are fixed, then locus of centre of variable circle will b an ellipse (a particular case would be of circle, when given circles are concentric)...
If C1 and C2 are not fixed, then the locus of centre would be a set of infinite ellipse'...
this is a diagramatic guess... i haven't solved anything yet...
let me know if i'm wrong...!!!
