1this is a really easy problem
at the orthocentre
just go to the basics of radical centre (intersection of racical axes)
and apply a bit geometry
The radical center of three circles described on three sides of triangle as diameeter is...............
-
UP 0 DOWN 0 0 3
3 Answers
1
1
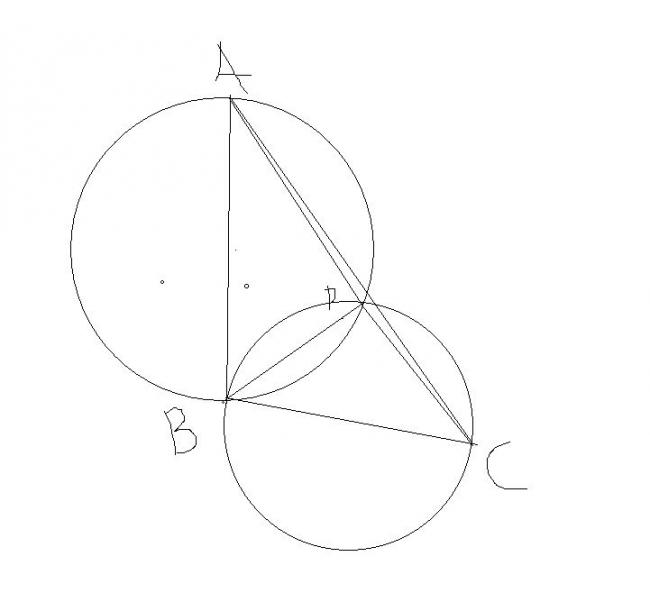
ok
see the figure
BP is one of those radical axes
As BP is common to bothe the circles
and BPC and APB both are semicircles
hence we get
√APB=90
and
√BPC=90
hence √APC=90+90=180
hence APC is a straight line
but there exists only one straight line between A and C
(the side AC)
hence BP is perpendicular to AC
thuse each radical axis is an altitude
hence the radical centre is the meeting point of the altitudes i.e circumcentre