ya itz ok....srry
15. Equation of a line is given by y+2at=t(x-at2), t being the parameter. Find the locus of the point of intersection of the lines which are at right angles.
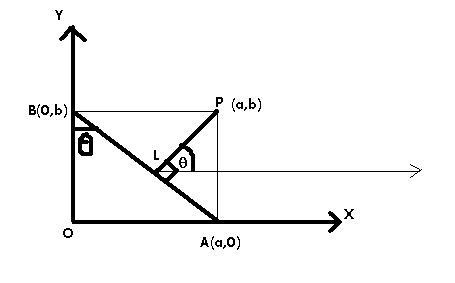
16.The ends A,B of a strait line line segment of a constant length 'c' slide upon the fixed rectangular axes OX & OY respectively. If the rectangle OAPB be completed then show that the locus of the foot of the perpendicular drawn from P to AB is X2/3+y2/3=c2/3.
-
UP 0 DOWN 0 0 10

10 Answers
15. Equation of a line is given by y+2at=t(x-at2), t being the parameter. Find the locus of the point of intersection of the lines which are at right angles.
take 2 lines of the same form:
\\y=tx-at^3-2at \\y=mx-am^3-2am \text{(Another parameter m)} \\0=(t-m)x-a(t-m)(t^2+tm+m^2)-2a(t-m) \\0=x-a(t^2+tm+m^2)-2a \\x=a(t^2+tm+m^2+2) \\y=a(t^2+tm+m^2+2)t-at^3-2at \\y=a(t^3+t^2m+m^2t+2t-t^3-2t) \\y=a(t^2m+m^2t)
the point of intersection is \left( a(t^2+tm+m^2+2) , a(t^2m+m^2t)\right)
now t and m are such that lines are perpendicular.. hence, tm=-1
substituting the same, we get \left( a(t^2+1/t^2+1) , a(t-1/t)\right)
If we eliminate t, we get
2\\\left( a(t^2+1/t^2+1) , a(t-1/t)\right) \\(y/a)^2=t^2+1/t^2-2 = x/a-3 \\(y/a)^2=x/a-3 \\y^2=ax-3a^2
a^2 + b^2 =c^2.......i
let L be (x1,y1)
L is the foot of perpendicular fom point P(a,b) on the line AB
eq of AB is bx+ay-ab=0
now sin theta = a/(a^2 +b^2)^(1/2)
cos theta =b/(a^2 +b^2)^(1/2)
using symmetric form of the line we get....
(x1-a)/(cos theta) +(y1-b)/(sin theta) =mod (ab +ab-ab)/(a^2 +b^2)^(1/2)
on putting value of cos theta and sin theta eq reduces to
(x1-a)/b =(y1-b)/a =-(ab +ab -ab)/(a^2 +b^2)
(x1-a)/b =(y1-b)/a =-ab/c^2
x1=a- {(a.b^2)/c^2} =a(c^2 -b^2)/c^2 =a^3/c^2
a^3=c^2.x1...........ii
similarly b^3=c^2.y1........iiii
using these relations ii & iii in eq i we get the required locus......
Some more ........
17 ) A straight line is drawn from the point(1,0) to the curve x2+y2+6x-10y+1=0, such that the intercept made on it by the curve subtends a right angle at the origin. Find the equations of the line.
18 )Show that all the chords of the curve 3x2-y2-2x+4y=0 which subtend a right angle at the origin are cincurrent. Does this result also hold for the curve, 3x2+3y2-2x+4y=0? if yes, what is the point of concurrency & if not, give reasons.
Q17 take eq of line as y=m(x-1)
now just homogenise the equation and put coefficient of x2+coefficient of y2=0
we get m=1,1/9
putting in equation of line
lines are y=1(x-1) and y=1/9(x-1)
Q18.................
let the eq of chord be lx + my =1
homogenizing 3x^2 -y^2 -2x+4y=0 with this eq we get
3x^2 -y^2+(-2x+4y)(lx+my)=0
i.e (3-2l)x^2 + (4m-1)y^2 + 4lxy=0........i
since lines given by eq i subtends a right angle at origin
so coefficient of x^2 + coefficient of y^2 =0
3-2l+4m-1=0
so l=2m+1
hence eq of such a chord is (2m+1)x+my=1
i.e x-1 +m(2x+y)=0
solving x-1=0
and 2x+y=0
we get that whatever may be the value of m ....point (1,-2) lies on this chord.......