Can u post ur method Aveek
9. A variable line, drawn through the point of intersection of the straight lines x/y + y/b = 1 & x/b + y/a =1, meets the coordinate axes in A & B. Show that the locus of the mid point of AB is the curve 2xy(a+b) = ab(x+y).
14. A triangle has side lengths 18,24 and 30. Find the area of the triangle whose vertices are the incenter, circumcentre and centroid of the triangle.
15. The points (1,3) & (5,1) are two opposite vertices of a rectangle. The other two vertices lie on the line Y= 2x+c. Find c & the remaining vertices.
19. Starting at the origin, a beam of light hits a mirror (in the form of a line) at the point A(4,8) and is reflected at the point B(8,12). Compute the slope of the mirror.
-
UP 0 DOWN 0 0 8

8 Answers
9. A variable line, drawn through the point of intersection of the straight lines x/y + y/b = 1 & x/b + y/a =1, meets the coordinate axes in A & B. Show that the locus of the mid point of AB is the curve 2xy(a+b) = ab(x+y).
use L1+λL2
you will get x(1/a+λ/b)+y(λ/a+1/b)=1+λ
Now the mid point of the poiont of intersection is given by
h=1+λ2(1/a+λ/b)
k = 1+λ2(λ/a+1/b)
all that is left is to elimilate lamda...
which can be done by taking 1/h and 1/k and adding them together
so 1/h+1/k=2(1/a+1/b)
hence the answer :)
14. A triangle has side lengths 18,24 and 30. Find the area of the triangle whose vertices are the incenter, circumcentre and centroid of the triangle.
this is a right angled triangle
u;se the properties.. the answer will not be very difficult..
to ease calculations, take the traingle of sides 3, 4, 5 and then multiply the result by 36 :)
15. The points (1,3) & (5,1) are two opposite vertices of a rectangle. The other two vertices lie on the line Y= 2x+c. Find c & the remaining vertices.
find the midpoint of the rectangle.. (3, 2)
length of the vertex from the mid point is given by root (5)
now the other points will be at parametric coordinates... such that one point is (3±√5x1/√5 , 2±√5x2/√5)
= (3±1, 2±2)
so (4, 4) and (2, 0)
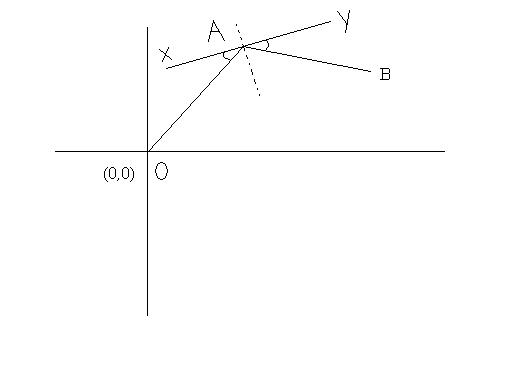
angles OAX=BAY
take their tangents
Let slope of XY = m
slopeOA = 2
slopeAB = 1
mod m-21+2m = mod m-11+m
If you consider +ve values, m2 = -1 which is rejected.
Take -ve values of the modulus.
Then solving the quadratic m will be 1±√103
Look carefully at the figure.....and make out that the line could not have been reflected to (8,12) if the slope had been -ve ,i.e, angle that XY made with the X-axis had been obtuse.
Hence it shows that XY makes an acute angle with the X-axis....slope +ve
Hence answer : 1+√103