should i give the explanation...?
the position vectors of point P nd Q re p and q respectively. if O is the origin and R is a point in the interior of angle POQ such that OR bisects the angle POQ then find the unit vector along OR
-
UP 0 DOWN 0 0 26

26 Answers
but abhishek ..
the resultant of those two unit vectors will not have magnitude √2
as angle between them is not equal to 90 ..
oh thnx varun............................... i never thought this simple concept.........heheh sorry all u guyz out dere........... thnx again varun..........................
z = a+ib.
arg(z) = θ
|z| = r.
we can write z as r(cosθ + isinθ).
z = reiθ.
I have made both p an q as unit vectors so they are equal :)
p/|p| =q/|q|
ok understood............so abhishek's method is wrong................fyn............tel me bout d formula........
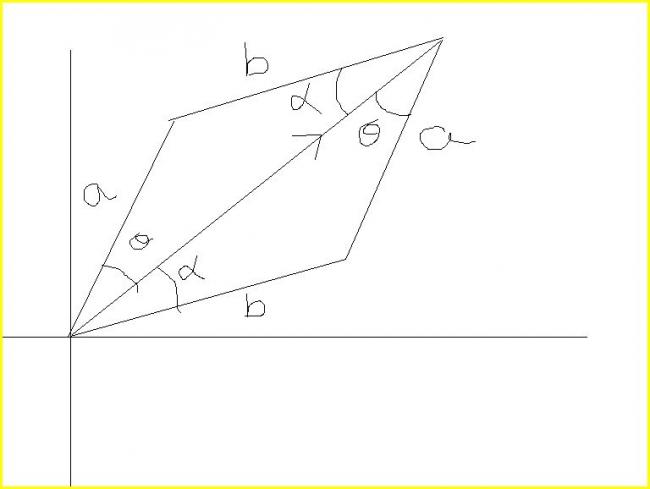
OK see the figure ..
if θ=α(as you r saying)
then see that both the triangles will be isoceles = >b=a
that means ,
only when b=a then only their addition will be along bisector
!!!!!
p=peiθ.................this wher is it???? ive never seen such formula.......
yes...........tel me how do v derive d formula..........goemetrical implicaions.................and in which book is tht formula in?????????
i think wat abhishek has done is rite................... wel i hav a doubt in ur method as i never saw ur eixwala formula.......... CUD BE RIGHT.............
but that will not give a vector along their bisector .. apply the parallelogram law and look
I just added the unit vectors in direction of p and q...... to get a vector in the bisector and make it a unit vector
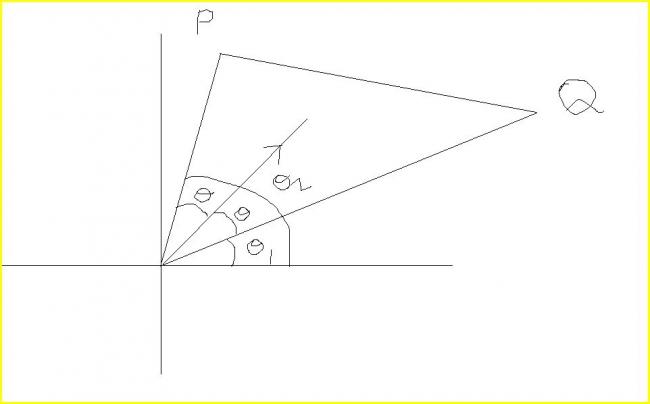
we can wrtie
θ1+θ+θ=θ2
hence θ=(θ2-θ1)/2
hence angular position of the bisector
θ1+θ = θ1+(θ2-θ1)/2 = (θ1+θ2)/2
and abhishek what method hv u used..
umm.. how do i say..
well see if you have two vectors of same length.
then, their resultant will be in the direction of their angular bisector as well
That is the funda you will have to use!
So the bisector of two vectors can be found by taking the resultant of the unit vectors !! (i mean replacing the old vectors by a unit vector)
but this does not guarantee that the resultant will be of the same length as a unit vector!
So we have to divide this resultant by its length!!
I dont knwo if this is what u were asking!
ok nishant all tht is fine...... i was just askin about the formula which he is used.......... hw did he get tht....???? i had never studied bout it..................... tht was my doubt......
Akand Complex and vectors and coordiante are all the same!! (in 2-D)
any vector (a,b) can be thought of as a+ib
and should try to use it as interchangably as possible.
When someone says point.. you should just jump to think.. which will be most useful.. COmplex point, vector point or coordinate point :)
ok rohan everything is understood.........just tell me hw did d first step cum???? if u tel me tht then everything else is ok.............. hw did u apply d concept of complex nums in vectors?????
oops it is asked to find unit vector
ok the solution -
p=|p|eiθ1
q=|q|eiθ2
that vector has an angle of (θ1+θ2)/2
pq=|p||q|ei(θ1+θ2)
√(pq/|p||q|) =ei(θ1+θ2)/2 (just taking root of both sides)
the above is the unit vector